【题解】2025 UESTC 暑假集训(div.1)
如梦似幻。
【7.9】 2025 上海市赛
用了 1h 意识到树形背包是 \(O(n^2)\) 的,太神奇了树形背包。
C. 饺子
令 \(f(x)\) 表示恰好吃 \(x\) 个饺子,能得到的最大愉悦值(忽略额外愉悦值 \(val\))。
容易看出,\(f(x)\) 是一个上凸函数,答案只能取在 \(0,m\) 和极值点三者之一。
对于某个取值点,可以使用 WQS 二分。二分斜率,对于一根固定斜率 \(k\) 的直线,找到与凸包的切点等价于最大化直线的截距,即 \(f(x)-kx\)。
而 \(f(x)=v_1+v_2+\cdots+v_x\),其中 \(v_i\) 为某个饺子带来的愉悦值,那么最大化 \(f(x)-kx=(v_1-k)+(v_2-k)+\cdots+(v_x-k)\) 也就等价于只取 \((v_i-k)\ge 0\to v_i\ge k\) 的饺子。
计算所有愉悦值 \(\ge k\) 的饺子带来的愉悦值之和,即为切点的纵坐标。
再考虑额外愉悦值 \(val\),这等价于将这个上凸函数的其中一段拉高,此时答案的取值点只可能增加了 \(l, r\) 两个点,同上求解。
时间复杂度 \(O(n\log w)\)。
E. Djangle 的数据结构
线段树维护:区间和,区间 \(\text{lcm}\),以及一个懒标记用于区间赋值。
可以说明,\(\gcd\) 操作时经过以下两个剪枝,复杂度就是对的:
- 如果 \(x\) 是当前区间 \(\text{lcm}\) 的倍数,此时直接返回区间和。因为 \(\gcd(a_i,x)=a_i\)。
- 如果区间所有数全相等(为 \(d\)),转换为区间赋值 \(\gcd(d,x)\)。
这是因为每次 \(\gcd\) 操作,\(a_i\) 的值至少减半,所以全局上看区间覆盖操作成功执行的次数的上界是 \(O(n\log w)\)。
而算上求 \(\gcd\),单次修改的成本是 \(O(\log n\log w)\),所以一共就 \(O(n\log n\log^2 w)\)。
要更加严谨的话需要势能分析。
【7.10】2020 ICPC Jinan Regional
只会 ez。
【7.11】2025 ICPC NAC
J. Popping Balloons
蓝色看成 \(0\),黄色看成 \(1\),红色看成 \(2\),问题变为每秒从序列中随机移除一个值,让序列变得有序的期望时间。
设随机变量 \(X\) 表示序列有序后剩下来的长度,则 \[ P(X\ge k)=\dfrac{f(k)}{\binom{n}{k}} \] 其中 \(f(k)\) 表示序列中长为 \(k\) 的非降子序列数量。
进一步 \[ E[X]=\sum_{k=1}^{n}P(x\ge k) \] 最终题目的答案就是 \(n - E[X]\)。
现在,问题只剩如何对 \(k\in [1,n]\) 求出 \(f(k)\)。
尝试用多项式描述信息。定义多项式 \(F_{L,R,i,j}(x)\),它 \(x^k\) 项的系数表示 “区间 \([L,R]\) 中,以 \(i\) 开头,\(j\) 结尾 \((0\le i\le j\le 2)\),长为 \(k\) 的非降子序列数量”。
这么定义的好处是,两个多项式相乘,\(x^i\) 的系数和 \(x^j\) 的系数会累加到新多项式 \(x^{i+j}\) 的系数上,意义就是两个区间合并,长为 \(i\) 的非降子序列和长为 \(j\) 的非降子序列会拼接成长为 \(i + j\) 的非降子序列。
先考虑基态。对于 \(a_i=x\ (x\in \{0,1,2\})\),\([x^1]F_{i,i,x,x}=1\),其它项均为 \(0\)。
再考虑合并。假设我们已经知道了区间 \([l,m]\) 的答案 \(F_{l,m,i,j}\) 和区间 \([m+1,r]\) 的答案 \(F_{m+1,r,i,j}\)(我们得到的是所有 \(i,j\) 的答案,换句话说,是一个 \(3\times 3\) 的多项式矩阵),那么 \[ \large F_{l,r,i,j}=\sum_{i\le p_1\le p_2\le j} F_{l,m,i,p_1}F_{m+1,r,p_2,j}+F_{l,m,i,j}+F_{m+1,r,i,j} \] 第一项表示拼接,后两项表示继承两侧区间的非降子序列数量。
分治 NTT 即可,最终 \(f(k)=\sum\limits_{i=0}^{2}\sum\limits_{j=0}^{2}[x^k]F_{1,n,i,j}\)。
时间复杂度 \(O(n\log^2 n)\)。
【7.12】毒瘤场 1
难炸了。
【7.15】牛客多校 1
【7.16】毒瘤场 2
难炸了。
【7.17】牛客多校 2
【7.18】杭电多校 1
B. 夜世界
有回溯操作,考虑可持久化线段树。
区间维护三个值:
- \(sum\):这一段的净收益(\(a_i-b_i\))。
- \(mn\):净收益(\(sum\))的前缀最小值。
- \(add\):从金矿获得的收益之和(\(a_i\))。
操作一和操作二就是普通的单点修改,操作三回溯,主要是操作四。
给出的 \(k\) 座金矿将 \([1,n]\) 划分成了 \(k + 1\) 段。
对一段区间 \([l,r]\),我们要解决:给一个初始金币数 \(x\),问从 \(l\) 走到 \(r\),手上的金币数变成了多少。
分两种情况:
- \(x+mn\ge 0\)。说明走在这段区间里手里一直有钱,走完后 \(x\) 变成 \(x+sum\)。
- \(x+mn<0\)。说明存在某个时刻手里没钱归零了,设此时在第 \(p\) 座金矿,最后手上的金币数就是 \(p\) 和 \(r\) 之间的净收益,数值上等价于 \(sum-mn\)。
解决了段内金币数怎么变,端点处金币数减半可以暴力修改。
最后,交给哥布林的金币数,就是当前版本下金矿的收益之和减去手上剩下的金币数。
时间复杂度 \(O((n+m+k)\log n)\)。
【7.19】Ucup2-20 Ōokayama
再也不想打小日子的场了。
【7.21】杭电多校 2
K. 10010
题面给的非常抽象。转化之后等价于:设当前询问区间为 \([l,r]\),区间内从右到左 \(1\) 的位置分别为 \(p_1,p_2,p_3,\ldots\),令 \(g_1=r-p_1\),\(g_2=p_1-p_2-1\),\(g_3=p_2-p_3-1\),\(\ldots\),则这段区间的得分为 \[ \large f([l, r])=g_1+\max_{g_1,g_2,\ldots,g_i\ \textbf{形成等差数列} }\ 3\cdot (i-1) \] 线段树,每个区间维护如下值。
- \(l\):左起第一个 \(1\) 的绝对坐标。
- \(r\):右起第一个 \(1\) 的绝对坐标。
- \(g\):右起第一个 \(1\) 和右起第二个 \(1\) 之间的间隔。
- \(ans\):右起构成等差数列的 \(1\) 的个数。
- \(cont\):区间里所有的 \(1\) 是否都属于右起的那个等差数列。
转移的时候,对于 \([l_1,r_1]\) 和 \([l_2,r_2]\),看 \(l_2-r_1-1\) 是否能作为一个间隔连接两段等差数列。
细节非常多,我写完之后对拍了很久才过。
ps:如果你维护了 “\(r\) 右侧 \(0\) 的个数”,那么大概率逻辑是不对的(
时间复杂度 \(O(n\log n)\)。
【7.22】牛客多校 3
P4389. 付公主的背包
考虑生成函数。其中 \(x^k\) 项的系数代表 “凑出体积为 \(k\) 的方案数”。
对于一个体积为 \(V\) 的物品,它能凑出的体积是 \(0,V,2V,3V,\cdots\),用多项式表示就是 \[ f_V(x)=x^0+x^V+x^{2V}+x^{3V}+\cdots \] 写成封闭形式(利用等比数列求和),就是 \(f_V(x)=\dfrac{1}{1-x^{V}}\)。
现在有 \(n\) 种体积为 \(v_1,v_2,\ldots,v_n\) 的物品,每种无限个,它们任意组合,凑出体积为 \(k\) 的方案数就是 \[ [x^k]\prod_{i=1}^{n}\frac{1}{1-x^{v_i}} \] 令 \(F(x)=\prod\limits_{i=1}^{n}\dfrac{1}{1-x^{v_i}}\),要算出 \(F(x)\) 前 \(m\) 项的系数,暴力把 个多项式乘起来是 \(O(nm\log m)\) 的。需要更快的方法。
令 \(G(x)=\ln F(x)\),也就是 \[ G(x)=\ln\prod\limits_{i=1}^{n}\dfrac{1}{1-x^{v_i}}=\sum_{i=1}^{n}\ln \left(\dfrac{1}{1-x^{v_i}}\right)=-\sum_{i=1}^{n}\ln(1-x^{v_i}) \] 但如果把 \(n\) 个 \(1-x^{v_i}\) 做多项式 \(\ln\),还是 \(O(nm\log m)\) 的。
这么转换的优势在,可以运用泰勒公式 \(\ln(1-u)=-(u+\frac{u^2}{2}+\frac{u^3}{3}+\cdots)=-\sum\limits_{i=1}^{\infty}\dfrac{u^i}{i}\)。
令 \(u=x^{v_i}\),有 \[ G(x)=-\sum_{i=1}^{n}\left(-\sum_{j=1}^{\infty}\frac{x^{j\cdot v_i}}{j}\right)=\sum_{i=1}^{n}\sum_{j=1}^{\infty}\dfrac{x^{j\cdot v_i}}{j} \] 对于一个体积为 \(v_i\) 的物品,它给 \(x^{v_i}\) 的系数贡献了 \(1\),给 \(x^{2v_i}\) 的系数贡献了 \(\dfrac{1}{2}\),给 \(x^{3v_i}\) 的系数贡献了 \(\dfrac{1}{3}\),以此类推。
我们记录有几种物品的体积为 \(v_i\),设为 \(p[v_i]\)。枚举 \([1,m]\) 内的每一种体积 \(i\),枚举 \(i\) 的倍数 \(j\),\(x^j\) 的系数就加上 \(p[i]\cdot i\)。这样一来,我们就在调和级数复杂度下计算出了 \(G(x)\) 前 \(m\) 项的所有系数。
利用多项式 \(\text{exp}\) 即可在 \(O(m\log m)\) 内还原出 \(F(x)\)。
I. Infinity
\(\nu(\sigma)\) 表示和 \(\sigma\) 共轭的置换的数量。
两个置换共轭,当且仅当它们拥有相同的轮换结构。
记 \(\lambda_i\) 表示 \(\sigma\) 长度为 \(i\) 的轮换个数,\(\sum\limits_{i=1}^{n}i\cdot \lambda_i=n\)。那么 \[ \nu(\sigma)=\frac{n!}{\prod\limits_{i=1}^{n}i^{\lambda_i}\cdot \lambda_i!} \] 其中 \(n!\) 是全集。对于 \(\lambda_i\) 个长度为 \(i\) 的轮换,每种轮换都有 \(i\) 种写法,比如 \((1\ 2\ 3)\),\((2\ 3\ 1)\),\((3\ 1\ 2)\) 实际上是相同的轮换,所以要除掉 \(i^{\lambda_i}\)。又因为这 \(\lambda_i\) 种轮换本身是不可区分的,所以还要除个 \(\lambda_i!\)。
那么,对于所有 \(n\) 阶置换构成的集合 \(S_n\),我们枚举每一种轮换结构 \(\{\lambda_i\}\),设这个轮换结构对应的置换是 \(\sigma_1,\sigma_2,\ldots \sigma_{\nu(\sigma)}\),其中 \(\nu(\sigma_1)=\nu(\sigma_2)=\ldots=\nu(\sigma_{\nu(\sigma)})\),取一个代表元 \(\sigma_1\),该轮换结构下所有置换的 \(\nu(\sigma_i)^k\) 之和,就是 \(\nu(\sigma_1)^{k+1}\)。
于是,答案为 \[ \sum_{\sum\limits_{i=1}^{n} i\cdot \lambda_i=n,\ 0\le \lambda_i\le n}\left(\dfrac{n!}{\prod\limits_{i=1}^{n}i^{\lambda_i}\cdot \lambda_i!}\right)^{k+1} \] 进一步,类似生成函数的组合意义,我们可以转换为多个幂级数相乘。 \[ (n!)^{k+1}[x^n]\prod_{i=1}^{n}\left(\sum_{j=0}^\infty \frac{x^{ij}}{(i^jj!)^{k+1}}\right) \] 相当于将所有 \(i\cdot j=n\) 的项取出来进行组合。
注意到 \[ \sum_{j=0}^\infty \frac{x^{ij}}{(i^jj!)^{k+1}} = \sum_{j=0}^\infty \frac{\left(\dfrac{x^i}{i^{k+1}}\right)^j}{(j!)^{k+1}} \] 故令 \[ F(x)=\sum_{j=0}^\infty \frac{x^j}{(j!)^{k+1}} \] 那么,答案是 \[ (n!)^{k+1}[x^n]\prod_{i=1}^{n}F\left(\dfrac{x^i}{i^{k+1}}\right) \] 现在,\(k\) 是固定的,有 \(t\) 次询问,每次问一个 \(1\le n\le 2\cdot 10^5\)。以下直接令 \(n=2\cdot 10^5\)。
令 \[ H(x)=\prod_{i=1}^{n}F\left(\dfrac{x^i}{i^{k+1}}\right) \] 我们肯定是想把 \(H(x)\) 构造出来,然后 \(O(1)\) 取它前 \(n\) 项的系数。
观察 \(H(x)\),是 \(n\) 个多项式相乘,就算每个多项式截断到 \(x^n\),乘起来也是 \(O(n^2\log n)\) 的。
类似付公主的背包,我们取 \(L(x)=\ln H(x)\),\(G(x)=\ln F(x)\),那么 \[ L(x) = \ln\prod_{i=1}^{n}F\left(\dfrac{x^i}{i^{k+1}}\right)=\sum_{i=1}^{n}\ln F\left(\dfrac{x^i}{i^{k+1}}\right)=\sum_{i=1}^{n}G\left(\dfrac{x^i}{i^{k+1}}\right) \] 其中,\(G(x)=\sum\limits_{i=0}^{n}g_ix^i\),有 \[ L(x)= \sum_{i=1}^{n}\sum_{j=0}^{n}g_j\left(\frac{x^{i}}{i^{k+1}}\right)^j = \sum_{i=1}^{n}\sum_{j=0}^{n}g_j\frac{x^{ij}}{i^{(k+1)\cdot j}} \] 到这里,我们就可以算出 \(L(x)\) 的前 \(n\) 项系数了。
对于每一对 \(i\cdot j = n\),为 \(x^{ij}\) 的系数贡献了 \(g_j \cdot i^{-j(k+1)}\)。而枚举每一对 \(i,j\) 的过程,是调和级数复杂度。
多项式 \(\text{exp}\) 即可求出 \(H(x)\) 的前 \(n\) 项系数。
时间复杂度 \(O(n\log n)\)。
【7.23】毒瘤场 3
终于可以看别人受苦了。
【7.24】牛客多校 4
烂完了。
I. I, Box
先判有无解。对于每一个连通块,如果 @ 的数目不等于
* 的数目,就无解,否则肯定有解。
策略是:每次选择一个 @,BFS 找到离它最近的
*。把这条路径拿出来,路径上可能还包括了多个 @
和 !,这些箱子按先后顺序编号为 \(a_1,a_2,\ldots,a_l\)。我们只需要将 \(a_{l-1}\) 移动到 \(a_l\),\(a_{l-2}\) 移动到 \(a_{l-1}\),\(\ldots\),\(a_{1}\) 移动到 \(a_2\)。
每次操作,推到位的箱子数都会多一个。不断这么操作,直到所有箱子都到位,时间复杂度显然不会超过 \(O(n^2m^2)\)。
【7.25】杭电多校 3
D. 三带一
二分答案,设二分出的答案是 \(mid\)。
设第 \(i\) 堆有 \(b_i\) 个形如 “XXX” 被使用,剩下 \(c_i=a_i-3b_i\) 个 “X”。
令 \(A=\sum a_i\),\(B=\sum b_i=mid\),\(C=\sum c_i=A-3\cdot mid\)。
首先,显然有
- \(\forall i\in [1,n]\),\(b_i\le \left\lfloor\dfrac{a_i}{3}\right\rfloor\)。
进一步,每个 “XXX” 都要匹配一个 “Y”(“X” \(\neq\) “Y”),那么
- \(\forall i\in [1,n]\),\(b_i\le \sum\limits_{j=1,j\neq i}^{n}c_j=C-c_i\)。
代入 \(c_i=a_i-3\cdot b_i\),得 \(b_i\ge \left\lceil\dfrac{a_i-(A-3\cdot mid)}{2}\right\rceil\)。
并且,还需要满足 \(B\le C\),即 \(mid\le A-3\cdot mid\),得 \(mid\le \left\lfloor\dfrac{A}{4}\right\rfloor\)。
综合一下,有 \[ \left[mid\le \left\lfloor\dfrac{A}{4}\right\rfloor\right]\land \left[\forall i\in [1,n],\ \left\lceil\dfrac{a_i-(A-3\cdot mid)}{2}\right\rceil\le b_i\le \left\lfloor\dfrac{a_i}{3}\right\rfloor\right] \] 对每一个 \(b_i\) 都能求出下界 \(l_i\) 和上界 \(r_i\)。
若 \(\exists i\),\(l_i>r_i\),或 \(mid<\sum l_i\),或 \(mid>\sum r_i\),就判定失败;否则判定成功。
时间复杂度 \(O(n\log w)\)。
【7.26】Ucup 3-3. Ukraine
H. Highway Hoax
任选一个点为根。
注意到对于一个点 \(u\),\(u\) 子树内 \(S\) 的个数当且仅当边 \((fa[u],u)\) 反转时会发生变化。
令 \(dp[u][0/1]\) 表示,在以 \(u\) 为根的子树中,有多少种合法的标号方案,使得边 \((fa[u],u)\) 保持初始方向 \(/\) 反转。
设 \(u\) 的儿子为 \(v_1,v_2,v_3,\ldots, v_m\),转移时,我们关注以所有 \(v_i\) 为根的子树中 \(S\) 的和。
假设我们已经求出了 \(dp[v][0/1]\),直接树形背包的时间复杂度显然无力应对,考虑生成函数。
尝试将 \(x^k\ (k\in \{-1,0,1\})\) 的系数表示为子树中 \(S\) 变化 \(k\) 个的方案数。举个具体的例子:
- 如果初始边 \((u,v_i)\) 的方向为 \(u\to v_i\),不反转 \(S\) 变化 \(0\) 个,反转后 \(S\) 变化 \(+1\) 个。
- 如果初始边 \((u,v_i)\) 的方向为 \(v_i\to u\),不反转 \(S\) 变化 \(0\) 个,反转后 \(S\) 变化 \(-1\) 个。
那么对于 \(u\to v_i\) 的情况,生成函数为 \(G_i(x)=dp[v_i][0]+dp[v_i][1]\cdot x\)。
对于 \(v_i\to u\) 的情况,生成函数为 \(G_i(x)=dp[v_i][0]+dp[v_i][1]\cdot x^{-1}\)。
这里有妙手,我们提一个 \(x^{-1}\) 出来,就变成 \(G_i(x)=x^{-1}(dp[v_i][1]+dp[v_i][0]\cdot x)\),这样两种情况形式就统一了。即,只需记一下乘了多少个 \(x^{-1}\)(或者说有多少条边方向是 \(v_i\to u\),记为 \(cnt\)),后面乘的时候就不用带上 \(x^{-1}\) 了。
令 \(F(x)=\prod\limits_{i=1}^{m}G_i(x)\),\(x^k\) 的系数就表示所有 \(v_i\) 的子树一共增加了 \(k+cnt\) 个 \(S\) 的方案数。这一步用分治 NTT 容易求出。
现在考虑状态转移。依靠的是 “\(u\) 的子树中 \(S\) 的变化量 \(=\) 节点 \(u\) 自身 \(S\) 的变化量(根据 \((fa[u],u)\) 是否反转可以是 \(-1,\ 0,\ 1\))\(+\) 所有 \(v_i\) 的子树中 \(S\) 的变化量之和”。
后者就是 \(F(x)\) 中的对应系数,分 “\(fa[u]\) 原本是 \(S\) 还是 \(F\)” 和 “\((fa[u],u)\) 是否反转” 进行转移即可。
时间复杂度 \(O(n\log^2 n)\)。
【7.28】杭电多校 4
HDU7503. Rikka 与子集 IV
任选一个点为根,比如 \(1\)。
令 \(dp[x][i]\) 表示以 \(x\) 为根的子树内,包含 \(x\) 且大小为 \(i\) 的连通子图个数,那么 \[ dp[x][i]=\sum_{i=j+k} dp[x][j]\cdot dp[y][k] \] 树形背包大多都能用生成函数优化。尝试将 \([x^j]F_i(x)\) 刻画为以 \(i\) 为根的子树中,包含 \(i\) 且大小为 \(j\) 的连通子图个数。那么 \[ F_i(x)=1+x\prod_{j\in \text{son}(i)}F_j(x) \] 开头加的 \(1\) 对应 \(dp[x][0]=1\),表示不选。
再令 \(S_i(x)=\sum\limits_{j\in \text{subtree}(i),\ j\neq i}F_j(x)\),答案就是 \([x^k](F_1(x)+S_1(x))\)。
直接算仍旧是 \(O(n^2\log n)\),考虑重链剖分。
令 \(s_i\) 表示点 \(i\) 的重儿子,我们的目标是找到 \(\{F_i(x),S_i(x)\}\) 和 \(\{F_{s_i}(x),S_{s_i}(x)\}\) 之间的递推关系。
令 \(G_i(x)=\prod\limits_{j\in \text{light}(i)}F_j(x)\),\(T_i(x)=\sum\limits_{j\in \text{light}(i)}(F_j(x)+S_j(x))\),那么 \[ \begin{align} F_i(x)&=1+x G_i(x) F_{s_i}(x)\\ S_i(x)&=T_i(x)+F_{s_i}(x)+S_{s_i}(x) \end{align} \] 写成矩阵形式,有 \[ \pmatrix{F_i(x) \\ 1\\ S_i(x)}=\pmatrix{xG_i(x) & 1 & 0 \\ 0 & 1 & 0 \\ 1 & T_i(x) & 1}\pmatrix{F_{s_i}(x) \\ 1 \\ S_{s_i}(x)} \] 边界情况是 \(F_{\text{leaf}}(x)=1+x\),\(S_{\text{leaf}}(x)=0\)。
于是,我们的策略是:
- 从根开始 dfs,一直走轻边,走到底回溯,首先叶子的 \(F\) 和 \(S\) 是知道的。
- 回溯的时候,对每个点 \(i\),分治 NTT 合并它所有轻儿子的 \(F\),得 \(G_i(x)\)。而 \(T_i(x)\) 也能通过普通的多项式加减得到。
- 如此一来,对于一条重链,我们知道了其上所有点的 \(G_i(x)\) 和 \(T_i(x)\)。换句话说,知道了重链上每个点的转移矩阵。
- 两个矩阵相乘相当于若干次多项式乘法。再次用分治 NTT 将这条重链上的所有矩阵合并。这一步基于矩阵具有结合律。
这样就求得了每条重链链顶的 \(F\) 和 \(S\)。
时间复杂度 \(O(n\log^2 n)\)。
HDU 的 submission 貌似只能看自己的,代码就贴下面好了。
#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "wb", stdout)
#define ck(x) { cout << "check " << x << endl;}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff
constexpr int mod = 998244353;
constexpr int G = 3; // 原根
int qpow(int k, int n) {
int s = 1;
for ( ; n; n >>= 1, k = k * k % mod) {
if (n & 1) s = s * k % mod;
}
return s;
}
// ---------- 多项式乘法 (NTT) ----------
vector<int> rev;
vector<int> rt{0, 1};
void dft(vector<int> &a) {
int n = a.size();
if ((int)rev.size() != n) {
int k = __builtin_ctz(n) - 1;
rev.resize(n);
for (int i = 0; i < n; i++) {
rev[i] = rev[i >> 1] >> 1 | (i & 1) << k;
}
}
for (int i = 0; i < n; i++) {
if (rev[i] < i) {
swap(a[i], a[rev[i]]);
}
}
if ((int)rt.size() < n) {
int k = __builtin_ctz(rt.size());
rt.resize(n);
while ((1 << k) < n) {
int e = qpow(G, (mod - 1) >> (k + 1));
for (int i = 1 << (k - 1); i < (1 << k); i++) {
rt[2 * i] = rt[i];
rt[2 * i + 1] = rt[i] * e % mod;
}
k++;
}
}
for (int k = 1; k < n; k *= 2) {
for (int i = 0; i < n; i += 2 * k) {
for (int j = 0; j < k; j++) {
int u = a[i + j];
int v = a[i + j + k] * rt[k + j] % mod;
a[i + j] = (u + v) % mod;
a[i + j + k] = (u - v + mod) % mod;
}
}
}
}
void idft(vector<int> &a) {
int n = a.size();
reverse(a.begin() + 1, a.end());
dft(a);
int inv = qpow(n, mod - 2);
inv = (inv + mod) % mod;
for (int i = 0; i < n; i++) {
a[i] *= inv;
a[i] %= mod;
}
}
vector<int> operator*(vector<int> a, vector<int> b) {
if (a.empty() || b.empty()) {
return {0};
}
int sz = 1, tot = a.size() + b.size() - 1;
while (sz < tot) {
sz <<= 1;
}
a.resize(sz);
b.resize(sz);
dft(a);
dft(b);
for (int i = 0; i < sz; i++) {
a[i] *= b[i];
a[i] %= mod;
}
idft(a);
a.resize(tot);
return a;
}
// ---------- 多项式加减、求导、积分 ----------
void shrink(vector<int> &a) {
while (a.size() > 1 && a.back() == 0) {
a.pop_back();
}
if (a.empty()) {
a.push_back(0);
}
}
vector<int> operator+(vector<int> a, const vector<int> &b) {
a.resize(max(a.size(), b.size()));
for (int i = 0; i < b.size(); i++) {
a[i] += b[i];
a[i] %= mod;
}
shrink(a);
return a;
}
vector<int> operator-(vector<int> a, const vector<int> &b) {
a.resize(max(a.size(), b.size()));
for (int i = 0; i < b.size(); i++) {
a[i] -= b[i];
a[i] = (a[i] + mod) % mod;
}
shrink(a);
return a;
}
vector<int> poly_deriv(vector<int> a) {
if (a.empty()) {
return {};
}
for (int i = 0; i + 1 < a.size(); i++) {
a[i] = a[i + 1] * (i + 1) % mod;
}
a.pop_back();
shrink(a);
return a;
}
vector<int> invt;
void pre_inv(int n) {
if (invt.empty()) {
invt.resize(2);
invt[1] = 1;
}
int sz = invt.size();
if (n <= sz) {
return;
}
invt.resize(n);
for (int i = sz; i < n; i++) {
invt[i] = (mod - invt[mod % i] * (mod / i) % mod) % mod;
}
}
vector<int> poly_integral(vector<int> a) {
if (a.empty()) {
return {};
}
int n = a.size();
pre_inv(n + 1);
a.push_back(0);
for (int i = n; i > 0; i--) {
a[i] = a[i - 1] * invt[i] % mod;
}
a[0] = 0;
shrink(a);
return a;
}
// ---------- 多项式求逆 (牛顿迭代法) ----------
vector<int> poly_inv(const vector<int> &a, int n) {
if (n == 0) {
return {};
}
vector<int> b = {qpow(a[0], mod - 2)};
int k = 1;
while (k < n) {
k <<= 1;
vector<int> c(a.begin(), a.begin() + min((int)a.size(), k));
c = c * b;
c.resize(k);
for (auto &x : c) {
x = mod - x;
}
c[0] = (c[0] + 2) % mod;
b = b * c;
b.resize(k);
}
b.resize(n);
return b;
}
// ---------- 多项式除法、取模、单点求值 ----------
pair<vector<int>, vector<int>> poly_div(vector<int> a, vector<int> b) {
shrink(a);
shrink(b);
int n = a.size();
int m = b.size();
if (n < m) {
return {{0}, a};
}
auto ar = a, br = b;
reverse(ar.begin(), ar.end());
reverse(br.begin(), br.end());
int len = n - m + 1;
auto br_inv = poly_inv(br, len);
auto qr = ar * br_inv;
qr.resize(len);
reverse(qr.begin(), qr.end());
auto qb = qr * b;
auto r = a - qb;
shrink(qr);
shrink(r);
return {qr, r};
}
vector<int> operator%(vector<int> a, vector<int> b) {
return poly_div(a, b).second;
}
int eval(const vector<int> &F, int x) {
int res = 0;
for (int i = F.size() - 1; i >= 0; i--) {
res = (res * x + F[i]) % mod;
}
return res;
}
// ---------- 多项式对数函数 O(NlogN) ----------
// 要求: a[0] == 1
vector<int> poly_log(vector<int> a, int n) {
assert(!a.empty() && a[0] == 1);
a.resize(n);
auto deriv_a = poly_deriv(a);
auto inv_a = poly_inv(a, n);
auto res = deriv_a * inv_a;
res.resize(n);
res = poly_integral(res);
res.resize(n);
return res;
}
// ---------- 多项式指数函数 O(NlogN) ----------
// 要求: a[0] == 0
vector<int> poly_exp(vector<int> a, int n) {
assert(a.empty() || a[0] == 0);
if (n == 0) {
return {};
}
vector<int> b = {1};
a.resize(n);
int k = 1;
while (k < n) {
k <<= 1;
auto log_b = poly_log(b, k);
vector<int> c(a.begin(), a.begin() + min((int)a.size(), k));
c.resize(k, 0);
for (int i = 0; i < k; ++i) {
c[i] = (c[i] - log_b[i] + mod) % mod;
}
c[0] = (c[0] + 1) % mod;
b = b * c;
b.resize(k);
}
b.resize(n);
return b;
}
// ---------- 多项式快速幂 O(NlogN) ----------
// 计算 A(x)^k mod x^n
vector<int> poly_pow(vector<int> a, int k, int n) {
shrink(a);
if (a.empty() || a.size() == 1 && a[0] == 0) {
return vector<int>(n, 0);
}
int d = -1;
for(int i = 0; i < a.size(); i++) {
if (a[i] != 0) {
d = i;
break;
}
}
if (d == -1 || d * k >= n) {
return vector<int>(n, 0);
}
int c = a[d];
int c_inv = qpow(c, mod - 2);
vector<int> ap(a.size() - d);
for(int i = 0; i < ap.size(); i++) {
ap[i] = a[i + d] * c_inv % mod;
}
ap = poly_log(ap, n);
for(auto &x : ap) {
x = x * k % mod;
}
ap = poly_exp(ap, n);
int ck = qpow(c, k);
vector<int> res(n, 0);
for(int i = 0; i + d * k < n && i < ap.size(); i++) {
res[i + d * k] = ap[i] * ck % mod;
}
return res;
}
// ---------- 多项式多点求值 O(Mlog^2M) ----------
vector<vector<int>> ptr;
void build_ptr(int p, int l, int r, const vector<int> &A) {
if (l == r) {
ptr[p] = {(mod - A[l]) % mod, 1};
return ;
}
int mid = l + r >> 1;
build_ptr(p << 1, l, mid, A);
build_ptr(p << 1 | 1, mid + 1, r, A);
ptr[p] = ptr[p << 1] * ptr[p << 1 | 1];
}
void calc_ptr(vector<int> F, int p, int l, int r, const vector<int> &A, vector<int> &res) {
if (r - l < 64) {
for (int i = l; i <= r; i++) {
res[i] = eval(F, A[i]);
}
return ;
}
F = F % ptr[p];
int mid = l + r >> 1;
calc_ptr(F, p << 1, l, mid, A, res);
calc_ptr(F, p << 1 | 1, mid + 1, r, A, res);
}
vector<int> multi_eval(const vector<int> &F, const vector<int> &A) {
if (A.empty()) {
return {};
}
int m = A.size();
ptr.assign(4 * m, {});
build_ptr(1, 0, m - 1, A);
vector<int> res(m);
calc_ptr(F, 1, 0, m - 1, A, res);
return res;
}
struct matrix {
int n, m;
vector<vector<vector<int>>> a;
matrix() {}
matrix(int n, int m) : n(n), m(m), a(n, vector(m, vector<int>{})) {}
};
matrix operator * (const matrix &x, const matrix &y) {
assert(x.m == y.n);
matrix z(x.n, y.m);
for (int k = 0; k < x.m; k++) {
for (int i = 0; i < x.n; i++) {
for (int j = 0; j < y.m; j++) {
if (x.a[i][k].empty() || y.a[k][j].empty()) {
continue;
}
z.a[i][j] = z.a[i][j] + x.a[i][k] * y.a[k][j];
}
}
}
return z;
}
//-------------- templates above --------------
void solve() {
int n;
cin >> n;
vector<vector<int>> adj(n + 1);
for (int i = 2; i <= n; i++) {
int x;
cin >> x;
adj[x].push_back(i);
}
vector<int> sz(n + 1, 1), son(n + 1);
auto dfs1 = [&] (auto self, int x) -> void {
int cnt = -1;
for (auto y : adj[x]) {
self(self, y);
sz[x] += sz[y];
if (sz[y] > cnt) {
cnt = sz[y];
son[x] = y;
}
}
};
dfs1(dfs1, 1);
vector<vector<int>> F(n + 1), S(n + 1);
auto dfs2 = [&] (auto self, int x) -> void {
for (int i = x; i; i = son[i]) {
for (auto y : adj[i]) {
if (y != son[i]) {
self(self, y);
}
}
}
vector<vector<int>> set_G, set_T;
for (int i = x; i; i = son[i]) {
vector<int> T;
vector<vector<int>> set_F;
for (auto y : adj[i]) {
if (y != son[i]) {
T = T + F[y];
T = T + S[y];
set_F.push_back(F[y]);
}
}
auto calc = [&] (auto self, int l, int r) -> vector<int> {
if (l == r) {
return set_F[l];
}
int mid = l + r >> 1;
return self(self, l, mid) * self(self, mid + 1, r);
};
vector<int> G;
if (set_F.empty()) {
G = {1};
} else {
G = calc(calc, 0, set_F.size() - 1);
}
set_G.push_back(G);
set_T.push_back(T);
}
auto calc = [&] (auto self, int l, int r) -> matrix {
if (l == r) {
matrix res(3, 3);
res.a[0][0] = set_G[l];
res.a[0][0].insert(res.a[0][0].begin(), 0);
res.a[0][1] = {1};
res.a[1][1] = {1};
res.a[2][0] = {1};
res.a[2][1] = set_T[l];
res.a[2][2] = {1};
return res;
}
int mid = l + r >> 1;
return self(self, l, mid) * self(self, mid + 1, r);
};
matrix leaf(3, 1);
leaf.a[0][0] = {1, 1};
leaf.a[1][0] = {1};
matrix res;
if (set_G.size() == 1) {
res = leaf;
} else {
res = calc(calc, 0, set_G.size() - 2) * leaf;
}
F[x] = res.a[0][0];
S[x] = res.a[2][0];
};
dfs2(dfs2, 1);
auto res = F[1] + S[1];
for (int i = 1; i <= n; i++) {
cout << (i < res.size() ? res[i] : 0) << " \n"[i == n];
}
}
signed main() {
fre(test);
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
solve();
}
return 0;
}【7.29】牛客多校 5
C. Array Deletion Game
结论:若 \(\sum\limits_{i=l+1}^{r-1}>s\),那么 \((l, r)\) 与 \((l+1, r-1)\) 胜负态相同。
- 若 \((l,r)\) 是必胜态 \(\to\) \(\{\)要么 \((l,r-1)\) 必败\(\}\) \((1)\) ,\(\{\)要么 \((l+1,r)\) 必败\(\}\) \((2)\)。
- \((1)\) 和 \((2)\) 都能推出 \((l+1,r-1)\) 必胜。
- 若 \((l,r)\) 是必败态 \(\to\) \(\{(l+1,r)\) 必胜\(\}\) \((3)\),且 \(\{(l,r-1)\) 必胜\(\}\) \((4)\)。
- \((3)\) 推出 \(\{\)要么 \((l+1,r-1)\) 必败,要么 \((l+2,r)\) 必败\(\}\) \((5)\)。
- \((4)\) 推出 \(\{\)要么 \((l+1,r-1)\) 必败,要么 \((l,r-2)\) 必败\(\}\) \((6)\)。
- 如果 \((5)\) 和 \((6)\) 中第一个子句有一个成立,那么 \((l+1,r-1)\) 必败。
- 否则 \(\{(l+2,r)\) 必败\(\}\) \((7)\),且 \(\{(l,r-2)\) 必败\(\}\) \((8)\)。
- \((7)\) 推出 \(\{(l+2,r-1)\) 必胜\(\}\) \((9)\),\((8)\) 推出 \(\{(l+1,r-2)\) 必胜\(\}\) \((10)\)。
- 假设 \((l+1,r-1)\) 是必胜态,那么推出 \(\{(l+2,r-1)\) 必败,或 \((l+1,r-2)\) 必败\(\}\),这与 \((9)(10)\) 矛盾。
- 因此,\((l+1,r-1)\) 必败。
得证。
因此,我们可以不断把序列两端各砍掉一个,直到当前 \(l', r'\) 满足 \(\sum\limits_{i=l'+1}^{r'-1}\le s\),即再两边砍一个就寄。
此时玩家只能不断从一边取数,胜负态确定。
具体的,设 \(fl\) 表示最大的下标,满足拿掉 \(fl\) 后 \((fl+1,r')\) 这一段就 \(\le s\);设 \(fr\) 表示最小的下标,满足拿掉 \(fr\) 后 \((l',fr-1)\) 这一段就 \(\le s\)。 先手必胜当且仅当 \(fl-l'\) 是奇数或者 \(r'-fr\) 是奇数。
对于一次询问,先一遍二分找出 \((l',r')\),再两遍二分找出 \(fl,fr\)。时间复杂度 \(O(q\log n)\)。
【7.30】NWERC 2024
放松场,做的貌似全是签到。剩个 B,队友补了就是我补了(确信
【7.31】牛客多校 6
发烧了,头很痛,没打。去校医院开了两盒药,一觉睡到晚上,随手点开题解里的一个 easy-mid,发现榜上只过了 20+,没绷住。
【8.1】Ucup3-18. SEERC 2024
感觉没 hdu 有意思,先补一下 hdu。
Lutece3353. A Boring Game
今日 hdu 的 A 题弱化,先写一下这题。
建出一棵 \((i, a_i)\) 大根笛卡尔树。
假设当前在点 \(i\),那么点 \(i\) 子树里的点肯定都能被攻破,相当于每次看 “利用当前子树里的所有资源,能否向根节点前进一步”。
具体的,令 \(S_x=\sum\limits_{y\in\text{subtree}(x)} b_y\),那么 \(x\) 能走到 \(fa_x\) 当且仅当 \(v+S_x\ge a_{fa_x}\),其中 \(v\) 表示角色的初始攻击力。
也就是说,当 \(a_{fa_x}-S_x> v\) 时,角色就无法继续移动了。对于一个询问 \((p,v)\),我们找到 \(p\) 到根节点的路径上第一个满足 \(a_{fa_x}-S_x>v\) 的点 ,答案就是 \(v+S_x\)。而找到 \(x\) 的过程可以用倍增实现。
时间复杂度 \(O(n\log n)\)。
A. 一个更无聊的游戏
上一题放到了树上。我们仍旧考虑建出 \((i,a_i)\) 大根笛卡尔树。
类似点分治的过程,找到最大的 \(a_i\),划分为若干子树,然后递归下去。
比较巧妙的做法是类似今年四川省赛,倒着考虑,按 \(a_i\) 从小到大枚举 \(i\),遍历 \(i\) 的邻居 \(j\),如果 \(j\) 被遍历过,就把 \(i\) 设为 \(j\) 所在连通块的根的祖先。
建出笛卡尔树后就和上一题无异了。
时间复杂度 \(O(n\log n)\)。
【8.2】Ptz Winter 2021 Day 8
今天脑子有点好,感觉写了很多题,不过还是没搞出 E,可惜。
F. Border Similarity Undertaking
分治。设当前处理的矩形为 \([l_1,r_1]\times [l_2,r_2]\)。如果 \(r_1-l_1>r_2-l_2\),我们就把矩形转一下,保证矩形的宽度大于高度,接着在中间砍一刀,分成 \([l_1,r_1]\times [l_2,mid]\) 和 \([l_1,r_l]\times [mid+1,r_2]\) 两部分,如此递归下去。
每次,我们计数 “左边界小于等于 \(y=mid\)” 且 “右边界大于等于 \(y=mid+1\)” 的矩形。
\(\forall i\in [l_1,r_1]\),扫描这一行,找到最小的 \(L[i]\) 和最大的 \(R[i]\),其中 \(l_2\le L[i]\le mid < R[i]\le r_2\),满足 \((i,L[i])\sim (i,R[i])\) 为同种字母。同样的,还要处理出 \(D[i][j]\) 表示 \((i,j)\) 向下最多能延伸多少格。
在中心线上,我们枚举待计数矩形的上下边界,贡献可以用前缀和 or 树状数组加速计算。
时间复杂度 \(O(nm\log nm)\)。代码里我图方便写的双 \(\log\),同样跑得飞快。
【8.4】杭电多校 6
前期题做的太慢了,1005 其实很简单但最后一小时二择的时候选了 1012。
1005. 钥匙迷宫
用大写字母表示锁,小写字母表示钥匙。
对于一组 \((X,x)\),容易看出:以 \(x\) 为根时,\(X\) 子树里的点的答案均为 \(0\)。可以用树上差分标记所有不能作为起点的 \(x\)。此时,剩下的能作为起点的 \(x\) 一定形成一个连通块(连通块里只有钥匙没有锁)。
从这些点出发 bfs,模拟开锁的过程,看是否能遍历完图上所有点。若能,则这些起点答案为 \(1\),其余为 \(0\);否则,答案全为 \(0\)。
时间复杂度 \(O(n\log n)\)。
1012. cats 的加减乘除
首先,一个符号位填入 + 和 -
的概率是均等的。意味着任何一段接在加减后的仅包含乘除的连续段,期望为
\(0\)。因此,整个表达式的期望等于从头开始的乘除连续段的期望。
分两步,第一步计算所有方案对应的表达式的值之和,第二步计算方案数(即有多少种不同的表达式),二者相除就是期望。
第二步是简单的,令 \(c=\sum [p_i=-1]\),答案是 \(c!\cdot 4^{n-1}\)。
对于第一步,枚举长度 \(i\),表示从头开始仅包含乘除的段的长度。设所有长为
\(i\) 的这样的段的表达式值之和为 \(\text{ans}[i]\),答案就是 \(\text{ans}[i]\times 2\times
4^{n-i-1}\)。意为这段紧接的是 + 或
-,而之后的符号随便填。
现在,题目转化为,对每个 \(i\in [1, n]\),求 \(\text{ans}[i]\)。
如果没有 \(p_i=-1\),则 \(\text{ans}[k]=a_1\prod\limits_{i=2}^{k}\left(a_i+\dfrac{1}{a_i}\right)\)。
如果存在 \(p_i=-1\),设有 \(m\) 个 \(-1\),这 \(m\) 个位置需要填入序列中没有的数,设这些将要填入的数分别为 \(b_1,b_2,\ldots,b_m\)。
发现如果 \(p_1=-1\),那将是特殊的,因为 \(p_1\) 不能是除数。
分类讨论。当 \(p_1\neq -1\) 时,令 \[ F(x)=\prod_{i=1}^{m}\left(1+\left(b_i+\dfrac{1}{b_i}\right)x\right) \] 填入 \(m\) 项中的 \(s\) 项,所有表达式的值之和即为 \([x^s]F(x)\)。这部分用分治 NTT 容易计算。
若 \(p_1=-1\),我们只能钦定 \(p_1\) 是什么,枚举所有 \(p_1\) 的可能取值并求和,答案是 \[ [x^s]\sum_{i=1}^{m}\dfrac{b_ix}{\left(1+(b_i+\frac{1}{b_i})x\right)}\prod_{i=1}^{m}\left(1+\left(b_j+\dfrac{1}{b_j}\right)x\right)\tag{*} \] 我们重点关注前面那个和式怎么算。
这个和式是 \(m\) 个一次分式相加,我们可以将其通分,具体的 \[ \dfrac{F_1(x)}{G_1(x)}+\dfrac{F_2(x)}{G_2(x)}=\dfrac{F_1(x)G_2(x)+F_2(x)G_1(x)}{G_1(x)G_2(x)} \] 等价于三次多项式乘法。我们可以沿用分治 NTT 的方法,将每个一次分式作为叶子,回溯时合并上去。
最后通分完分母可以与 \((*)\) 式右侧约去,只剩下分子。当然就算你没注意到也只不过多一次多项式求逆而已。
时间复杂度 \(O(n\log^2 n)\)。
【8.5】牛客多校 7
今天过题过得特别快,剩个 H,队友补了就是我补了(确信
【8.6】Ucup3-35. Kraków
F 挺有意思,但是不太会,等 dwdyy 会了教我(躺
【8.7】牛客多校 8
【整体二分】
适用:单个询问可以二分解决,询问能离线,询问间没有顺序依赖。
做法:对值域二分,通常是四元组 \((l, r, \{p\},\{q\})\),表示当前研究的询问的答案在 \([l, r]\) 内,\(\{p\}\) 是当前要考虑的元素/修改操作的集合,\(\{q\}\) 是当前要考虑的询问集合。
很难说得清怎么做。下面是静态区间第 \(k\) 小的板子。
void solve() {
int n, m;
cin >> n >> m;
vector<array<int, 2>> p;
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
p.push_back({x, i});
}
vector<array<int, 4>> q;
vector<int> ans(m);
for (int i = 0; i < m; i++) {
int l, r, k;
cin >> l >> r >> k;
q.push_back({l, r, k, i});
}
Fenwick fen(n);
auto dfs = [&] (auto self, int l, int r,
vector<array<int, 2>> &p,
vector<array<int, 4>> &q) -> void {
if (l == r || q.empty()) {
for (auto [_, __, k, i] : q) {
ans[i] = l;
}
return ;
}
int mid = l + r >> 1;
vector<array<int, 2>> pl, pr;
vector<array<int, 4>> ql, qr;
for (auto &cur : p) {
auto &[val, i] = cur;
if (val <= mid) {
pl.push_back(cur);
fen.add(i, 1);
} else {
pr.push_back(cur);
}
}
for (auto &cur : q) {
auto &[L, R, k, i] = cur;
int res = fen.query(L, R);
if (k <= res) {
ql.push_back(cur);
} else {
k -= res;
qr.push_back(cur);
}
}
fen.clear();
self(self, l, mid, pl, ql);
self(self, mid + 1, r, pr, qr);
};
dfs(dfs, 0, 1e9, p, q);
for (auto x : ans) {
cout << x << "\n";
}
}H. 区间 LRU
令 \(pre[i]\) 表示 \(a_i\) 上一次出现的位置,\(f[i]\) 表示区间 \([pre[i]+1,i-1]\) 中不同的数的个数。
运用树状数组容易预处理出全部的 \(f[i]\),详见 Link。
对于第一种类型的询问,相当于问 \([l, r]\) 中有多少个 \(i\),满足 \(pre[i]\ge l\) 且 \(f[i]<k\)。
对于第二种类型的询问,相当于问 \([l,r]\) 中 \(f[i]\) 的第 \(k\) 小值。
整体二分,对于当前四元组 \((l,r, \{p\},\{q\})\),按右端点 \(r\) 升序遍历所有询问,将所有 \(p[i]\le r\),\(f[p[i]]\le mid\) 的 \(i\) 对应的 \(pre[i]\) 加进树状数组。后面就是标准的处理了。
时间复杂度 \(O(n\log^2 n)\)。
【8.8】杭电多校 7
倒闭 +1。
1002 想了个和题解完全不同的做法,很麻烦,所以还是补一下正解。
QOJ9904. 最小生成树
很有意思的题。
暴力的做法是:将 \(a_i\) 从小到大排序,假设当前为 \(a_k\),我们可以用并查集将所有 \(i+j=k\) 且不在一个连通块的 \((i,j)\) 连起来,支付 \(a_k\) 的代价。
我们考虑加速这个过程。对于一个固定的 \(k\),所有 \(i+j=k\) 的 \((i,j)\) 需要满足 \(1\le i\le n,\ 1\le j=k-i\le n\),也就是 \(\max(1,k-n)\le i\le \min(n,k-1)\),我们将这个区间称作 \([l,r]\)。
在这个区间里,每一对 \((i,j)\) 都关于 \(\dfrac{k}{2}\) 对称,也就是 \((l, r)\),\((l+1,r-1)\),\((l+2,r-2)\),\(\ldots\) 这样组合。
做最小生成树时,我们会用并查集连边,令 \(f_i\) 表示点 \(i\) 所在连通块的根。
观察:将所有 \(i+j=k\) 的 \((i,j)\) 全连起来后,区间 \([l, r]\) 对应的 \(f\) 数组回文。
我们反复 check 区间 \([l, r]\),如果不回文,就二分找到第一个不回文的位置,并查集连起来,累加 \(a_k\) 的贡献。
具体的,线段树维护正串哈希值和反串哈希值,二分一个固定的长度 \(p\),判断 \([l,r]\) 内长为 \(p\) 的前缀的正串和长为 \(p\) 的后缀的反串是否相等。
因为生成树只用连 \(n-1\) 次,只会执行 \(O(n)\) 次二分,每次线段树 check,总复杂度 \(O(n\log^2 n)\)。
另有单 \(\log\) 的做法,占坑。
1011. 切披萨
离线整体二分。
为了方便之后切上凸壳,预先对点集(以下称 \(\{p\}\))按 \(x\) 坐标从小到大排序,询问(直线集合,下称 \(\{q\}\))按斜率 \(\left(-\dfrac{A}{B}\right)\) 从小到大排序,斜率相同优先截距 \(\left(\dfrac{C}{B}\right)\) 大的。
对于当前四元组 \((l,r,\{p\},\{q\})\),将编号小于等于 \(mid\) 的询问分进 \(\{ql\}\),否则分进 \(\{qr\}\)。
问题是 \(\{p\}\) 要如何划分。一个点被分进 \(\{pl\}\) 当且仅当它在某一条 \(\{ql\}\) 内的线段下方。
单调栈切出 \(\{ql\}\) 的上凸壳,不仅记录组成上凸壳的每条直线的信息,还要处理出上凸壳上每个交点的横坐标,这样就可以按 \(x\) 坐标从小到大遍历 \(\{p\}\) 中的每个点,双指针移动到凸壳上对应的直线,判断当前点是否满足 \(Ax+By\le C\)。满足的分到 \(\{pl\}\),否则分到 \(\{pr\}\)。
算交点横坐标时,可以直接取整数,因为 \(\{p\}\) 中均为整点。举个例子,若真实的 \(x=5.7\),你取 \(x’=5\),那么满足 \(y\le x\) 的 \(y\) 也满足 \(y\le x'\);满足 \(y>x\) 的 \(y\) 也满足 \(y>x'\)。
时间复杂度 \(O(n\log n)\)。注意不要输出行末空格,问就是 hduoj 特性。
1002. 龙族栖息地
观察可得,两点 \((q_1,r_1,s_1),(q_2,r_2,s_2)\) 间的最短距离是 \(\dfrac{|q_1-q_2|+|r_1-r_2|+|s_1-s_2|}{2}\)。
设核心房间的坐标是 \((x,y,-x-y)\),那么任务是最小化 \[
f(x,y)=\sum_{i=1}^{n}\left(|x-q_i|+|y-r_i|+|-x-y-s_i|\right)
\] 对于一个固定的 \(x\),寻找
\(y\) 使得 \(f(x,y)\) 最小是一个经典问题。结论是 \(y\) 取 \(\{r_1,r_2,\ldots,r_n,-x-s_1,-x-s_2,\ldots,-x-s_n\}\)
这 \(2n\) 个数的中位数是最优的。利用
std::nth_element 可以线性取出。
但枚举每一个 \(x\) 复杂度依然很大。注意到 \(f(x,y)\) 展开式中的三项每一项都关于 \(x,y\) 二维下凸,求和后依然二维下凸。因此,三分找到最优的 \(x\) 即可。
时间复杂度 \(O(n\log w)\)。
【8.9】Ptz Summer 2020 Day 3
挺有意思的场,可补的题挺多的。
C. Count on a Tree II Striking Back
\(f(a,b)\ge 2f(c,d)\) 或 \(f(c,d)\ge 2f(a,b)\) 是一个重要的突破点。
考虑随机化,对于 \(k\) 个 \([0,1]\) 内的实数随机变量,最小值的期望是 \(\dfrac{1}{k+1}\)。
我们对每一种颜色随机一个整数,称作哈希值。对于一次询问 \((a,b,c,d)\),令 \(g(a,b)\) 表示 \(a,b\) 两点的简单路径上每个点对应颜色的哈希值的最小值。如果 \(g(a,b)<g(c,d)\),我们就能估计 \(f(a,b)>f(c,d)\)。
将上述看成一次试验,为保证正确性,我们要进行 \(B\) 次试验,在这 \(B\) 次试验中,每次都为所有 \(n\) 种颜色重新分配哈希值。
令 \(S_{a,b}\) 表示 \(B\) 次试验中 \(g(a,b)\) 之和,若 \(S_{a,b}<S_{c,d}\),就判定 \(f(a,b)>f(c,d)\),此时错误率已经足够低。
建出 \(B\) 棵线段树跑重链剖分,时间复杂度 \(O(nB+mB\log^2n)\)。
【8.11】杭电多校 8
1001. 最遥远的路
考虑单个询问 \([ql, qr]\) 怎么做。
令 \(dp[x]\) 表示以 \(x\) 结尾的最长路径长度。按边权 \(w\) 从小到大的顺序依次枚举 \(w\in [ql, qr]\) 的边转移,有 \[ dp[y]=\max_{(x,y,w,d)}dp[x]+d \] 若初始 \(dp[i]=0,\ dp[\text{others}]=-\infty\),得到的就是以 \(i\) 为起点,\(x\) 为终点的最长路径长度。
线段树分治。对于线段树上一个点 \([l, r]\),存储所有跨过 \(\dfrac{l+r}{2}\) 的询问。对于一个询问 \([ql, qr]\),将其拆分到线段树上的 \(\log\) 个节点上,二分确定每个节点对应该询问的边界。
分治计算时,设当前为 \((l, r)\),枚举 \(1\sim n\) 中的每个点 \(i\) 作为中转点,在 \(\text{mid}\) 两侧分别 dp,算出:\(d1[x]\) 表示 \((l,\text{mid})\) 中以 \(x\) 为起点,\(i\) 为终点的最长路径长度;\(d2[x]\) 表示 \((\text{mid} + 1,r)\) 中以 \(i\) 为起点,\(x\) 为终点的最长路径长度。这样,对于当前节点的每一组询问 \([ql, qr]\),就能用如下式子更新答案。 \[ \max_{i=ql}^{\text{mid}} d1[i]+\max_{j=\text{mid}+1}^{qr}d2[j] \] 时间复杂度 \(O(nm\log m+q\log m)\)。
1002. 不最近的路
先考虑在题给的新定义下如何求最短路。
直接做并不好做,注意到图的边权很小,我们可以枚举边权第 \(k\) 大的边的权值。
算法流程如下,感性理解是容易的,详细证明可以看官方题解。
- 枚举边权第 \(k\) 大的边的权值 \(v\)(包括 \(v=0\))。
- 将每条边 \((x,y,w)\) 的边权 \(w\) 重新设置为 \(w'=\max(0,w-v)\)。
- 跑 Dijkstra,得到 \(dis_v[i]\),表示从点 \(1\) 到各个点的距离。
- 新定义下 \(1\to n\) 的最短路权值即为 \(\min\limits_{v}dis_{v}[n]+kv\)。
如何求次短路?实际上,次短路仍然可以通过上述算法求出,只不过要求 “和求出的最短路不完全重合”。
为此,我们在跑 Dij 时顺便记录如下两个信息:
- \(\text{pre}[y]=x\):表示 \(y\) 的上一步由 \(x\) 转移而来。
- \(\text{nxt}[y]=i\):其中 \(i\) 是边 \((x,y)\) 的编号,这条信息就表示 \(y\) 从 \(x\) 的哪条出边转移而来。
你可能认为只用记录其中一个就行了,但实际上你要考虑次短路可以经过同一个点两次。杭电的数据很水,实测只记录 \(\text{nxt}\) 就能 AC,一眼随的。
令 \(\text{dis}[x][1]\) 表示到达 \(x\) 的路径完全是第一步算出的最短路的一个前缀,\(\text{dis}[x][0]\) 表示当前到 \(x\) 的路径已经偏移了最短路,松弛的时候就是: \[ \text{dis}[y][f']=\min_{f'=f\ \land\ \text{nxt}[y]=i\ \land \ \text{pre}[y]=x} \text{dis}[x][f]+w \] 初态 \(\text{dis}[1][1]=0\),答案就是 \(\text{dis}[n][0]\)。
时间复杂度 \(O(m^2\log m)\)。
【8.12】牛客多校 9
简单场,但烂完了。
I. Tree Construction
考虑一个简化的问题:给定一棵树的 \(\text{dis}[i][j]\),能否还原出树的结构?
答案是肯定的。将所有 \(n^2\) 组 \(\text{dis}[i][j]\) 从小到大排序,每次并查集合并不在同一连通块的两点,最终得到的最小生成树即为所求。原理是:相邻的点因为边权更小,会优先合并。
回到这题,注意到无论 \(\text{d1}[i][j]\) 和 \(\text{d2}[i][j]\) 怎么交换,\(\text{d}1[i][j]+\text{d}2[i][j]\) 都是定值。于是,我们将 \(\text{d}1[i][j]+\text{d}2[i][j]\) 作为 \((i,j)\) 的边权,跑最小生成树,就能还原树的结构。原理是:相邻的点同样因为 \(\text{d}1[i][j]+\text{d}2[i][j]\) 更小,会优先合并。
接下来,要确定 \(\text{d1}[i][j]\) 和 \(\text{d2}[i][j]\) 如何分配到两棵树上(称为树 \(T_1\) 和树 \(T_2\))。我们任取一点为根 dfs,当前边为 \((u,v)\),不妨先假设 \(w_1=\text{d1}[u][v]\) 属于 \(T_1\),\(w_2=\text{d2}[u][v]\) 属于 \(T_2\),然后遍历已经经过的点,看有没有冲突的地方。有冲突,就交换 \(w_1\) 和 \(w_2\)。
时间复杂度 \(O(n^2\log n)\)。
【8.13】Ucup3-21. Ōokayama
好难的场。
M. Cartesian Trees
考虑给每个询问的区间 \([l, r]\) 搞出一个哈希值,这样只用统计有多少不同的哈希值。
如果两个区间的笛卡尔树同构,哈希值必须相同。我们要想办法提取出一个区间的特征。
令 \(L[i]\) 表示 \(i\) 左侧最近的 \(<a_i\) 的位置,\(R[i]\) 表示 \(i\) 右侧最近的 \(<a_i\) 的位置。
一个想法是,对于一个区间 \([l,r]\),我们保存所有满足 \(l\le L[i]<i\le r\) 的 \(i-L[i]\)(这表示笛卡尔树上左子树的大小),并按 \(i\) 升序保存它们,得到一个列表 \(\{i_1-L[i_1],i_2-L[i_2],\ldots\}\ (i_1<i_2<\ldots)\),称作 \(f_1[l,r]\)。
同样的,对于所有满足 \(l\le i<R[i]\le r\) 的 \(R[i]-i\)(这对于笛卡尔树上右子树的大小),按 \(i\) 升序保存它们,得到 \(\{R[i_1]-i_1,R[i_2]-i_2,\ldots\}\ (i_1<i_2<\ldots)\),称作 \(f_2[l,r]\)。
两个区间 \([l_1,r_1],[l_2,r_2]\) 的笛卡尔树同构,当且仅当 \(f_1[l_1,r_1]=f_1[l_2,r_2]\) 且 \(f_2[l_1,r_1]=f_2[l_2,r_2]\)。而对于不同构的两个区间,两个等号必有一个不能取到。
于是,我们将二元组 \((f_1[l, r], f_2[l, r])\) 作为区间 \([l, r]\) 的哈希值是合适的。
怎么对所有 \(Q\) 个区间求出哈希值?我们将每个 \(i-L[i]\) 和 \(R[i]-i\) 看作一个字符,查询一段区间的 \(i-L[i]\) 的列表就相当于用字符串哈希询问一个区间的哈希值。
将所有询问离线,扫描线,对于一组 \((L[i],i)\),我们在 \(i\) 时刻将 \(i-L[i]\) 的单点哈希值加进树状数组的 \(L[i]\) 位置。\((i,R[i])\) 同理。
时间复杂度 \(O(n\log n)\)。
【8.14】牛客多校 10
罚时吃得最饱的一场。疑似凌晨 4 点睡导致脑子一团浆糊,狂暴 wa 了四发才醒过来。
水母,嘿嘿嘿。海星,嘿嘿嘿。鳗鱼,嘿嘿嘿。
【8.15】杭电多校 9
三开大失败。虽然我 1007 已经想清楚了,但脑瘫写了个可能会退化到 \(O(n^2)\) 的东西。
不过赛后发现即便改过来了,map<array<int, 2>, int>
的常数还是很大。
又狂 T 了十几发之后,终于发现开 \(n\) 个 map<int, int>
会大幅减小常数,之后才过。
挺好的题,从 Link 里学到了怎么找到三角剖分里的所有三角形,并为每条有向线段找到逆时针方向的三角形顶点编号。非常巧妙,代码也很短,感谢 Diaosi 的指导。
1007. 三角剖分
首先,任意简单多边形的任一三角剖分的对偶图是一个 “任一节点度数至多为 \(3\)” 的树。也就是说,当你选定任意一点为根,呈现出的是一棵二叉树。
我们可以在这棵树上进行 dp。当然,也可以不显式把树建出来,直接分治求解。
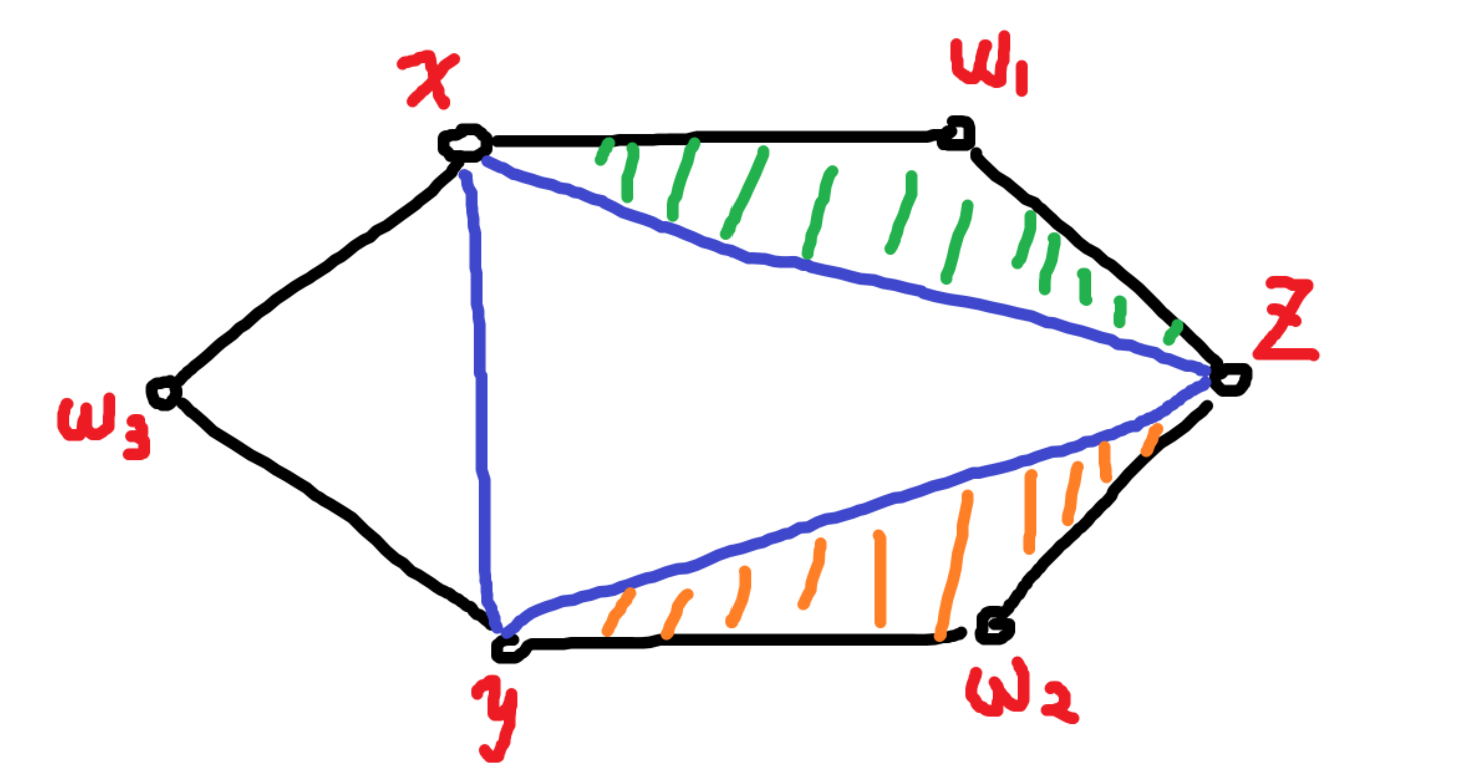
如上图,以对角线 \((x,y)\) 为例,在 \((x,y)\) 右侧(或者说 \(\overrightarrow{xy}\) 的逆时针方向),所在三角形是 \(xyz\),我们可以把问题递归到边 \((x,z)\) 和 \((z,y)\)。而 \((x,z)\) 逆时针方向是三角形 \(xzw_1\),我们又可以递归到 \((x,w_1)\) 和 \((w_1,z)\)。此时已经到了多边形边界,递归停止。
为方便表述,定义 \(S(x,y)\) 表示 \(\overrightarrow{xy}\) 与其逆时针方向的凸多边形边界围成的子多边形。例如,图中 \(S(x,y)\) 就表示多边形 \(xyw_2zw_1\),而 \(S(y,x)\) 就表示多边形 \(yxw_3\)。定义 \(p(x,y)\) 表示 \(\overrightarrow{xy}\) 逆时针方向的三角形顶点编号,对于图中就是 \(p(x,y)=z\),\(p(y,x)=w_3\)。接下来我们就可以开始 dp 了。
令 \(f_{S(x,y)}\) 表示 \(S(x,y)\) 中生成树的数量。
令 \(g_{S(x,y)}\) 表示 \(S(x,y)\) 中恰有两个连通分量,且 \(x\) 和 \(y\) 不在一个连通分量的生成森林的数量。
初态:当 \(S(x,y)\) 为多边形的一段边界时,\(f_{S(x,y)}=g_{S(x,y)}=1\)。
令 \(z=p(x,y)\),转移如下 \[ \begin{align} g_{S(x,y)} &=f_{S(x,z)}\cdot g_{S(z,y)}+f_{S(z,y)}\cdot g_{S(x,z)}\\ f_{S(x,y)} &= f_{S(x,z)} \cdot f_{S(z,y)}+g_{S(x,y)} \end{align} \] 解释一下:先看第一个式子,\(f_{S(x,z)}\cdot g_{S(z,y)}\) 表示从 \(S(x,z)\) 中选取一个完整的生成树,再从 \(S(z,y)\) 中选取 \(z\) 和 \(y\) 不在一个连通分量的一个生成森林,这样 \(z\) 所在的连通分量通过点 \(z\) 并入了 \(S(x,z)\) 的生成树,而 \(x,y\) 依然处于不同的连通分量。另一部分同理。
再看第二个式子,\(f_{S(x,z)} \cdot f_{S(z,y)}\) 表示 \(S(x,y)\) 中不经过边 \((x,y)\) 的生成树数量,而 \(g_{S(x,y)}\) 恰好表示经过边 \((x,y)\) 的生成树数量(将原本不在同一连通分量的 \(x\) 和 \(y\) 所在的连通分量用边 \((x,y)\) 连起来,得到一棵生成树)。
至此,我们可以枚举每条对角线,向两侧递归,得到所有的 \(f_{S(x,y)}\) 和 \(g_{S(x,y)}\)。使用记忆化搜索,每个 \(S(x,y)\) 的答案至多只会算一次,所以是单 \(\log\) 的。
对于一个询问 \((x,y)\),我们要算去掉对角线 \((x,y)\) 后的生成树数量,答案是 \[ (f_{S(x,y)}-g_{S(x,y)})\cdot g_{S(y,x)}+(f_{S(y,x)}-g_{S(y,x)})\cdot g_{S(x,y)} \] 时间复杂度 \(O(n\log n)\)。
【8.16】Ucup3-4. Hongō
倒闭,怎么 A 是模拟题,C 感觉没这么简单但也过了一车。
【8.18】杭电多校 10
怎么只有我们队在打。
1001. Submission
对于一个人 \(x\),设 \(p_1,p_2,\ldots, p_l\) 表示 \(x\) 的提交对应的下标。我们将 \(x\) 留在大脑中的时刻表示成区间,称为 “保留区间”,区间的左右端点只有是 \(p_i\) 时才有用。例如,\([p_1,p_3],[p_4,p_8]\) 表示第一次「仔细阅读」后,第二第三次提交都因 \(x\) 还在大脑中而被跳过,接着 \(x\) 被踢出大脑,于是在第四次提交时再次「仔细阅读」,之后第五到第八次提交都被跳过。
Observation. 每个人 \(x\) 对应的 “保留区间” 都只有一个,且形如 \([p_1,p_i]\)。
注:严谨来说是 \([p_1,p_i],[p_{i+1},p_{i+1}],[p_{i+2},p_{i+2}],\ldots,[p_l,p_l]\)。在以下叙述中,单点构成的区间均被略去。
Proof. 假设 \(x\) 有两个 “保留区间”,形如 \([p_1,p_i],[p_j,p_k]\ (i<j)\)。当 \(x\) 在 \((p_i,p_{i+1})\) 被驱逐,意味着有另一个不在大脑中的人 \(y\),试图进入大脑,并且 \(x\) 的优先级是大脑里所有 \(k+1\) 个人(包括 \(y\))中最低的。在不断挤占的过程中,大脑里 \(k\) 个位置对应的人的优先级只升不降。如果 \(x\) 在之后的某个时刻再次进入大脑,他的优先级仍旧是 \(k\) 个位置中最低的,当下一个人想进来,被驱逐的就一定是 \(x\)。此时的收益远不如在一开始就将 \(x\) 的优先级调高,使其形成一个更长的保留区间 \([p_1,p_k]\)。
于是,问题转化为:有 \(m\) 个人,每个人有若干形如 \([p_1,p_i]\),收益为 \(i-1\) 的区间(\(p_2\sim p_i\) 被跳过),你要为每个人选择恰好一个区间,使得总收益最大,约束是数轴上所有形如 \(i.5\) 的位置的被覆盖次数 \(\le k\)。
考虑费用流,建模如下。四元组 \((u,v,f,c)\),其中 \(f\) 是容量,\(c\) 是费用。\(p_{i,j}\) 表示 \(i\) 第 \(j\) 次出现的位置。
- \(\forall i\in [1,n-1]\),\((i,i+1,k,0)\)
- \((S,1,k,0)\),\((n,T,k,0)\)
- \(\forall i\in [1,m]\),\((p_{i,1},n+i,1,0)\)
- \(\forall p_{i,j\ (j\ge 2)}\),\((n+i,p_{i,j},1,j-1)\)
当然,我们不可能对所有 \(k\in [1,m]\) 都跑一次费用流。经典的套路是把所有容量为 \(k\) 的边的容量都重新设置为 \(m\),每次跑一条增广路出来。
时间复杂度,\(O(4031\texttt{ms})\)。
【尾声】
第二次来清水河集训了,相比第一次,最大的变化可能是学子 mai 取代了朝阳二楼的位置(笑哭
简单回忆,收获比较大的是与生成函数,分治有关的一点技巧,但也只是一点皮毛。
比较难忘的是前期若干和重链剖分有关的题,以及最后的三角剖分。
另有若干题没来得及补,例如两道倍增并查集的题。说实话,暑假一过我大概率就没什么动力去补了。