【题解】六月训练日记
QOJ9748. 最大公因数的平方和
由莫比乌斯反演,令 \(g(n)=n^2=\sum\limits_{d\mid n}f(d)\),则 \(f(n)=\sum\limits_{d\mid n}\mu(d)g\left(\dfrac{n}{d}\right)=\sum\limits_{d\mid n}\mu(d)\left(\dfrac{n}{d}\right)^2\)。
我们可以在调和级数复杂度内预处理出所有的 \(f(n)\)。
于是,原式化为 \[ \begin{align} \sum_{i=l}^{r}\sum_{j=L}^{R}\gcd(a_i,b_j)^2 &=\sum_{i=l}^{r}\sum_{j=L}^{R}\sum_{d\mid \gcd(a_i,b_j)}f(d)\\ &=\sum_{i=l}^{r}\sum_{j=L}^{R}\sum_{d\mid a_i\land d\mid b_j}f(d)\\ &=\sum_{d=1}^{n}f(d)\sum_{i=l}^{r}[d\mid a_i]\sum_{j=L}^{R}[d\mid b_j] \end{align} \] 后两项形式相同,我们以 \(\sum\limits_{i=l}^{r}[d\mid a_i]\) 为例,相当于问一段区间内有多少个数是某个值 \(d\) 的倍数。
阈值分治,设阈值为 \(B\)。那么当 \(d\le B\) 时,我们可以对每个 \(d\) 处理出一个前缀和,这样每个询问就可以 \(O(1)\) 查询。这部分是 \(O(nB+qB)\) 的。
而 \(d>B\) 时,把这个倍数在 \(\{a\}\) 中的下标记作 \(i\),在 \(\{b\}\) 中的下标记作 \(j\)。可以看成如下二维数点问题:
- 二维平面上有若干个点,每个点的坐标是 \((i,j)\),有一个权值 \(f(d)\)。
- 有若干询问,每个询问形如:在一个矩形区域内所有点的权值和。
利用分块进行二维数点,这部分是 \(O(\dfrac{n^2}{B^2}+q\sqrt{n})\) 的。
QOJ9476. 012 Grid
先引用四张官方题解的图片。
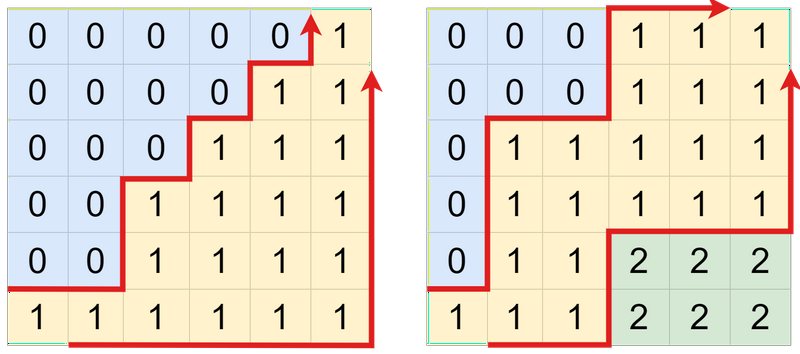
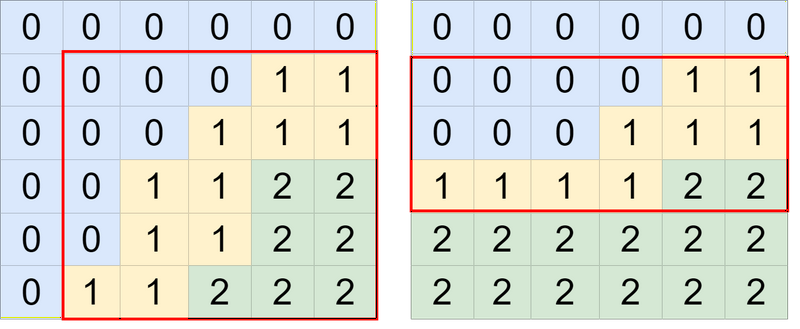
不难发现,题目的约束等同于找两条从左下到右上的路径,这两条路径分别分割了 \(0/1\) 以及 \(1/2\),严格不相交。其中前两幅图路径起点都是 \((0,1)\) 和 \((1,0)\),终点都是 \((n, m-1)\) 和 \((n-1,m)\)。而后两幅图可以提取出一个子矩形(红圈框起来),只研究这个子矩形的话和前两幅图无异。
于是我们先研究前两幅图的情况。回忆 LGV 引理,有向无环图上,给定 \(k\) 个起点 \(\{a_1,a_2,\ldots,a_k\}\) 和 \(k\) 个终点 \(\{b_1,b_2,\ldots,b_k\}\),那么要满足 \(a_i\to b_i\) 这 \(k\) 条路径严格互不相交,方案数是: \[ \det\pmatrix{e(a_1,b_1) & e(a_1,b_2) & \cdots & e(a_1,b_k)\\ e(a_2,b_1) & e(a_2,b_2) & \cdots & e(a_2,b_k)\\ \vdots & \vdots & \ddots & \vdots\\ e(a_k,b_1) & e(a_k,b_2) & \cdots & e(a_k,b_k) } \] 其中 \(e(a_i,b_j)\) 表示从 \(a_i\) 到 \(b_j\) 所有路径的权重之和。再者,一条路径的权重定义为路径上所有边权之积。于是,当图中所有边权都是 \(1\) 时,\(e(a_i,b_j)\) 就等价于从 \(a_i\) 到 \(b_j\) 有多少条不同的路径。再回忆,网格图上,如果只朝右或朝上走(这样相当于有向无环图),那么从点 \(P(x_1,y_1)\) 到 \(Q(x_2,y_2)\) 有 \(\dbinom{|x_1-x_2|+|y_1-y_2|}{|x_1-x_2|}\) 种不同的走法(插板法),故 \(e(P,Q)= \dbinom{|x_1-x_2|+|y_1-y_2|}{|x_1-x_2|}\)。
回到本题,\(k=2\),起点分别为 \((0,1),(1,0)\),终点分别为 \((n,m-1),(n-1,m)\),那么严格不相交路径数等于 \[ \det\pmatrix{\dbinom{n+m-2}{n} & \dbinom{n+m-2}{n-1}\\ \dbinom{n+m-2}{n-1} & \dbinom{n+m-2}{m} } = \frac{(n+m-2)!(n+m-1)!}{n!m!(n-1)!(m-1)!} \] 这个组合数展开花了我相当多的时间,可能需要一点技巧(
好,现在我们看向后两幅图,我们现在要枚举那个红框框起来的区域。观察这两幅图,左边这幅子矩形贴着右侧和下侧,我们称这种情况为 "右下",同理右边这幅是 "左右" 的情况。
于是,共有左上、右下、左右、上下四种情况,后两种比较平凡,枚举矩形的长/宽,乘这样尺寸的矩形有几个,再累加即可。
对于前两种,矩形的长和宽都需要枚举,相当于求一个这样的式子 \[ \sum_{i=1}^{n}\sum_{j=1}^{m}\frac{(i+j-2)!(i+j-1)!}{i!j!(i-1)!(j-1)!} \] 分子的形式引起我们注意,令 \(p=i+j\),原式化为 \[ \sum_{p=2}^{n+m}(p-2)!(p-1)! \sum_{i+j=k} \underbrace{\frac{1}{i!(i-1)!}}_{\Large f_i} \cdot \underbrace{\frac{1}{j!(j-1)!}}_{\Large g_j} \] 后面那项用 NTT 卷积即可。
时间复杂度 \(O((n+m)\log (n+m))\)。
QOJ9479. And DNA
定义 \(f_n(m)\):长度为 \(n\) 的序列 \(\{a\}\),满足 \(\forall i\in [1,n]\),\(a_i+(a_{i-1}\&a_{i+1})=m\) 的序列数量。
先思考 \(m\) 比较小的情况。
当 \(m=0\) 时,只有全 \(0\) 序列能满足要求,故 \(f_n(0)=1\)。
当 \(m=1\) 时,\(\{a\}\) 只能是 \(01\) 序列。根据定义易知 \(\{a\}\) 需要满足 "没有连续两个 \(0\)" 且 "没有连续三个 \(1\)"。
这等价于在下述状态机中,从任意一个顶点出发,经过 \(n\) 条边回到同一顶点的路径条数。
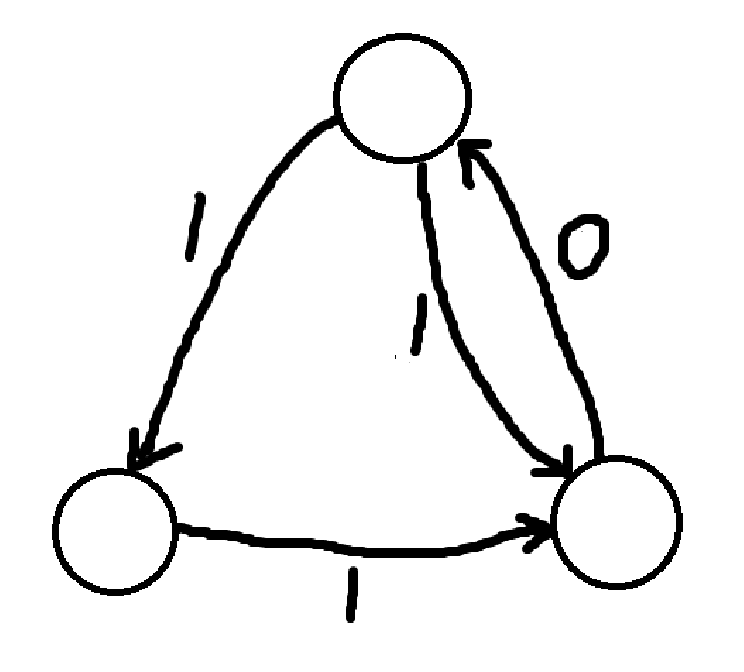
邻接矩阵配合矩阵快速幂,可以在 \(O(\log n)\) 内解决。
当 \(m\) 为 \(\ge 2\) 的偶数时,草稿纸上画一下,易知此时 \(\{a\}\) 要么全是偶数,要么全是奇数。
- 当 \(\{a\}\) 全为偶数时,令 \(a_i=2b_i\),方程变为 \(2b_i+(2b_{i-1}\&2b_{i+1})=m\)。由位运算的性质,括号里的 \(2\) 可以提出来,于是方程化为 \(b_i+(b_{i-1}\&b_{i+1})=\dfrac{m}{2}\)。这是一个规模更小的问题,即 \(f_n(\dfrac{m}{2})\)。
- 当 \(\{a\}\) 全为奇数时,令 \(a_i=2b_i+1\),代入方程,同样能推导出 \(b_i+(b_{i-1}\&b_{i+1})=\dfrac{m}{2}-1\)。
故 \(f_n(m)=f_n(\dfrac{m}{2})+f_n(\dfrac{m}{2}-1)\)。
当 \(m\) 为 \(\ge 3\) 的奇数时,换一个视角,在计算 \(a_i+(a_{i-1}\&a_{i+1})\) 时二进制下最低位一定不会产生进位。
这允许我们将最低位和高位部分分开计算,两部分独立,方案数可以乘起来。
- 最低位部分,\(a_i^{(low)}+(a_{i-1}^{(low)}\&a_{i+1}^{(low)})=1\),即 \(f_n(1)\)。
- 高位部分,把末尾的 \(1\) 除掉之后剩下 \(\dfrac{m-1}{2}\),即 \(f_n(\dfrac{m-1}{2})\)。
故 \(f_n(m)=f_n(1)\times f_n(\dfrac{m-1}{2})\)。
时间复杂度 \(O(\log n+\log m)\)。
QOJ9488. Do Not Turn Back
将 "不连续走同一条边" 的条件称为 \((*)\) 条件。
定义一个 \(N\times N\) 的方阵 \(X_k\):\(X_k[i][j]\) 表示从 \(i\) 到 \(j\) 长度为 \(k\) 且满足 \((*)\) 的路径数量。
于是答案即为 \(X_k[1][n]\)。
同样定义以下几个 \(N\times N\) 的矩阵:
- \(A\):图 \(G\) 的邻接矩阵。
- \(D\):图 \(G\) 的度数矩阵。(对角矩阵,对角线上的元素为对应顶点的度数)
- \(I\):单位矩阵。
- \(O\):零矩阵。
接下来看怎么推导出 \(X_k\)。
当 \(k=1\) 时,显然有 \(X_1=A\)。
当 \(k=2\) 时,若不考虑 \((*)\),答案是 \(A^2\)。而不满足 \((*)\) 的路径形如 \(i\to j\to i\),这样的路径有 \(\text{deg}(i)\) 条,于是 \(X_2=A^2-D\)。
当 \(k\ge 3\) 时,同样考虑从 \(AX_{k-1}\) 中减去不满足 \((*)\) 的部分。
考虑 \(AX_{k-1}\) 的含义是所有长度为 \(k-1\) 的合法路径再往前走一步。对于一条路径: \[ a_0\to \ldots \to a_{k-3}\to a_{k-2}\to a_{k-1} \] 不满足 \((*)\) 的路径形如,从 \(a_{k-2}\) 开始走一段 \(i\to j\to i\ (i=a_{k-2})\)。其中 \(j\) 的选择有 \(\text{deg}(i)-1\) 种,减一是因为前面的路径合法保证了 \(j\) 不能是 \(a_{k-3}\)。于是,不满足 \((*)\) 的路径数有 \((D-I)X_{k-2}\) 这么多。
也就是说,\(X_k=AX_{k-1}-(D-I)X_{k-2},\ k\ge 3\)。
写成矩阵快速幂的形式 \[ \pmatrix{X_k\\X_{k-1}}=\pmatrix{A & -(D-I)\\ I & O}\pmatrix{X_{k-1}\\ X_{k-2}} \] 即 \[ \pmatrix{X_k\\X_{k-1}}=\pmatrix{A & -(D-I)\\ I & O}^{k-2}\pmatrix{X_2\\ X_1} \] 时间复杂度 \(O(N^3\log K)\)。
QOJ10346. Make Triangle
令 \(S=\sum x_i\),三个集合分别为 \(A, B, C\),则题目可以转化为给出 \(\{x\}\) 的一个三集合划分使得 \(|A|=n_a\),\(|B|=n_b\),\(|C|=n_c\) 且 \(\min\left(\sum\limits_{x\in A}x,\sum\limits_{x\in B}x,\sum\limits_{x\in C}x\right) < \dfrac{S}{2}\)。
在以下叙述中,默认 \(x_1\le x_2 \le \ldots\le x_n\) 且 \(n_a\le n_b\le n_c\)。
下面是一些必要条件
- 最大的元素不能太大:\(x_n+\sum\limits_{i=1}^{n_a-1}x_i<\dfrac{S}{2}\)。
- 最大的组要装得下最小的几个元素:\(\sum\limits_{i=1}^{n_c}x_i<\dfrac{S}{2}\)。
可以证明这个条件是充分的。但我们选择证明一个比上述条件更强的引理。
Lemma. 如果我们按 \(\{x_i\}\) 从大到小选择它们应该放进的集合(即当前需要放置的元素比任何已经在集合里的元素都要小),设 \(n'\) 表示还没放的数的个数(即 \(x_1,x_2,\ldots,x_{n'}\)),\(n_a'\),\(n_b'\),\(n_c'\) 表示三个集合的剩余容量(满足 \(n_a'+n_b'+n_c'=n'\)),\(S_a\),\(S_b\),\(S_c\) 表示三个集合已经装进的数的和,则剩下的这 \(n'\) 个数能合法塞进三个集合的充要条件是:
- \(\exists g\in \{a,b,c\}\),\(S_g+x_{n'}+\sum\limits_{i=1}^{n_g'-1}x_i<\dfrac{S}{2}\)。
- \(\forall g\in \{a,b,c\}\),\(S_g+\sum\limits_{i=1}^{n_g'} < \dfrac{S}{2}\)。
Prove. 必要性显然,这里证充分性。我们不妨令集合 \(A\) 满足第一个条件,那么 \(S_a+x_{n'}+\sum\limits_{i=1}^{n_a'-1}x_i<\dfrac{S}{2}\)。
此时将 \(x_{n'}\) 放进 \(A\) 中,剩下的 \(x_1\sim x_{n'-1}\) 任意放进 \(B,C\) 中。设如此操作后有 \(S_a'\),\(S_b'\) 和 \(S_c'\),则若 \(S_b'<\dfrac{S}{2}\) 且 \(S_c'<\dfrac{S}{2}\),那么我们就已经找到了一组合法划分。否则,\(\max(S_b',S_c')\ge \dfrac{S}{2}\),不失一般性,我们令 \(S_b'\ge \dfrac{S}{2}\)。
此时,\(S_a'+S_c'<\dfrac{S}{2}\),我们可以任意交换 \(A,C\) 中的元素(除 \(x_{n'}\) 外)。现在,观察如果任意交换 \(B,C\) 中的元素,会发生什么情况。在一次交换中,换进 \(C\) 的元素 \(<x_{n'}\),换出 \(C\) 的元素 \(\ge 1\),那么 \(C\) 中元素的和最多增长 \(x_{n'}-1\)。而交换前 \(S_c'\le S-S_b'-S_a'\le \dfrac{S}{2}-S_a'\le \dfrac{S}{2}-x_{n'}\)。
意思是,交换后 \(S_c''\le S_c'+(x_{n'}-1)\le \dfrac{S}{2}-x_{n'}+(x_{n'}-1)<\dfrac{S}{2}\)。
也就是说,\(B,C\) 也可以任意交换,再加上 \(A,C\) 可以任意交换,所有元素都可以在三个集合之间调整,直到 \(S_b'<\dfrac{S}{2}\)。又因为 Lemma 的第二个条件的存在,保证了一定能调整出来。故该引理得证。
好的,现在我们拥有了这个 Lemma,做法也就呼之欲出了:从大到小分配 \(\{x\}\) 中的元素,逐一尝试分配到 \(A,B,C\) 中,看一下某次尝试后,Lemma 的条件是否满足。若满足,就分配。若无论分配到哪一个集合都无法满足 Lemma,就无解。
时间复杂度 \(O(n)\)。
QOJ9851. Cup of Water
设每个回合倒的水量是 \(U_i\),那么 \(U_i\sim \text{Unif}(0,x)\)。
记 \(n\) 个回合后倒水量的总和为 \(S_n=U_1+U_2+\ldots+U_n\)。
定义随机变量 \(N\) 表示首次将桶装满所需的回合数,我们要求的就是 \(E[N]\)。
因为第 \(n\) 次装满 \(\to\) 前 \(n-1\) 次都没装满,所以 \[ E[N]=\sum_{n=1}^{\infty}P(S_{n-1}<1)\longrightarrow E[N]=\sum_{n=0}^{\infty}P(S_n<1)\tag{1} \] 令 \(U_i=x\cdot V_i\),则 \(V_i\sim \text{Unif}(0,1)\)。那么 \[ S_n < 1\longrightarrow x\sum_{i=1}^{n}V_i<1\longrightarrow \sum_{i=1}^{n}V_i<\frac{1}{x} \] 这是 Irwin-Hall 分布,详情见 link。
结论是,对于 \(n\) 个在 \([0,1]\) 内均匀分布的实数随机变量,它们的和不超过一个实数 \(z\) 的概率 \[ P\left(\sum V_i < z\right)=\frac{1}{n!}\sum_{k=0}^{\lfloor z\rfloor}(-1)^k\binom{n}{k}(z-k)^{n} \] 在这里 \(z=\dfrac{1}{x}\),即 \[ \begin{align} P(S_n<1) &=\frac{1}{n!}\sum_{k=0}^{\lfloor 1/x\rfloor}(-1)^k\binom{n}{k}\left(\frac{1}{x}-k\right)^{n}\\ &=\frac{1}{n!x^n}\sum_{k=0}^{\lfloor 1/x\rfloor}(-1)^k\binom{n}{k}(1-kx)^{n} \end{align} \] 代回 \((1)\) 中,调整求和顺序,有 \[ \begin{align} E[N] &=\sum_{n=0}^{\infty}\frac{1}{n!x^n}\sum_{k=0}^{\lfloor 1/x\rfloor}(-1)^k\binom{n}{k}(1-kx)^{n}\\ &=\sum_{k=0}^{\lfloor 1/x\rfloor}(-1)^k\sum_{n=0}^{\infty}\frac{1}{n!x^n}\binom{n}{k}(1-kx)^{n}\tag{2} \end{align} \] 注意到 \(n<k\) 时 \(\dbinom{n}{k}=0\),所以第二个求和号实际是从 \(n=k\) 开始。
我们不妨单独拎出来 \[ \sum_{n=k}^{\infty}\frac{1}{n!x^n}\binom{n}{k}(1-kx)^{n} \] 令 \(m=n-k\),即 \(n=k+m\),代入。这么做是因为要将求和下界重新调整为 \(0\)。
同时将组合数展开,有 \[ \begin{aligned} &\ \ \ \ \sum_{m=0}^\infty \frac{1}{(k+m)!\,x^{k+m}} \cdot\frac{(k+m)!}{k!\,m!}\,(1-kx)^{k+m}\\ &=\sum_{m=0}^\infty \frac{(1-kx)^{k+m}}{k!\,m!\,x^{k+m}}\\ &=\frac{(1-kx)^k}{k!\,x^k} \sum_{m=0}^\infty\frac{\left(\frac{(1-kx)}{x}\right)^{m}}{m!}\\ &=\frac{(1-kx)^k}{k!\,x^k}\, \exp\left(\frac{1-kx}{x}\right) \end{aligned} \] 最后一步是幂级数展开,\(e^x=\sum\limits_{i=0}^{\infty}\dfrac{x^i}{i!}\)。
代回 \((2)\),最终有 \[ E[N] =\sum_{k=0}^{\lfloor1/x\rfloor} (-1)^k\, \frac{(1-kx)^k}{k!\,x^k}\, \exp\left(\frac{1-kx}{x}\right) \] 因为 \(x\ge 0.05\),所以 \(\left\lfloor\dfrac{1}{x}\right\rfloor \le 20\),很小,直接暴力算这个式子即可。
单组数据几乎是 \(O(1)\) 的。
QOJ9853. Easy String Problem
定义 \(S(l, r)\) 表示割掉 \([l, r]\) 后得到的串,即 \(\overline{a_1a_2\ldots a_{l-1}a_{r+1}\ldots a_n}\)。
结论:若 \(\exists k\),\(S(l,r)=S(l+k,r+k)\),那么 \(\forall i\in [0,k]\),\(S(l, r)=S(l+i,r+i)\)。
纸上画一下还是比较显然的。
那么,对于一组询问 \((L,R)\),我们相当于求有多少对 \((l,r)\),满足 \(l\le L\le R\le r\),且 \(S(l,r)\neq S(l-1,r-1)\)。
容斥,这等价于 \(L\cdot(n-R+1)\) 减去 \(S(l,r)=S(l-1,r-1)\) 的 \((l,r)\) 对数。
而 \(S(l,r)=S(l-1,r-1)\) 又当且仅当 \(a_{l-1}=a_r\)。
所以我们实际要求有多少对 \((l,r)\) 满足 \(1\le l\le L-1\),\(R+1\le r\le n\) 且 \(a_l=a_r\)。
用莫队求解。
具体的,维护 \(\text{inL}[x]\) 和 \(\text{inR}[x]\) 表示在当前区间左侧/右侧的 \(x\) 个数,边界移动时贡献是好算的。
时间复杂度 \(O(n\sqrt{n})\)。
QOJ9855. Glass Bead Game
拆贡献期望题。
注意到当轮数到达无穷时,珠子初始位置其实并不重要,即某个珠子出现在某个位置的概率是固定的。
我们要求的是按给定概率选中一个玻璃珠,将它往前移动的期望代价。
而代价定义为在当前珠子前面的珠子个数,故定义 \[ X_{i,j}= \begin{cases} 1 &, \text{选中第 } i \text{ 个珠子并且第 } j \text{ 个珠子在第 } i \text{ 个珠子前面}\\ 0 &, \text{otherwise}\\ \end{cases} \] 设答案为 \(X\),那么 \[ X=\sum_{i\neq j} X_{i,j} \] 由期望的线性性 \[ E[X]=E\left[\sum_{i\neq j}X_{i,j}\right]=\sum_{i\neq j}E[X_{i,j}]\tag{1} \] 根据 \(X_{i,j}\) 的定义,令事件 \(A\) 为选中第 \(i\) 个珠子,事件 \(B\) 为移动第 \(i\) 个珠子时,第 \(j\) 个珠子在其前面,两个事件相互独立。则 \[ E[X_{i,j}]=P(X_{i,j}=1)=P(A\cap B)=P(A)P(B)\tag{2} \] 其中 \(P(A)=p_i\),而 \(P(B)\) 可以如下考虑。
我们只关心第 \(i\) 个珠子和第 \(j\) 个珠子的相对位置,移动其它珠子不会改变这个相对位置,所以我们可以考虑只包含这两个珠子的模型。什么时候 \(j\) 会在 \(i\) 前面,无非是上一步选中了 \(j\) 往前移,这个概率等于 \[ P(B)=\frac{p_j}{p_i+p_j} \] 代回 \((2)\),\((2)\) 再代回 \((1)\),有 \[ E[X]=\sum_{i\neq j}\frac{p_ip_j}{p_i+p_j} \] 时间复杂度 \(O(n^2)\)。
数据范围略微诈骗,不知道有没有其它复杂度的做法。
QOJ9860. Light of Stars
\(k\) 很小,可以每个扇区分开计算。
对于一个点 \(P_i(x_i,y_i)\),它能被 \(P_j(x_j,y_j)\) 照射到,当且仅当方向向量 \(\overrightarrow{P_jP_i}=(x_i-x_j,y_i-y_j)\) 在扇区内。
分别取扇区两条边界线上两点 \(A(\cos\alpha,-\sin\alpha)\) 和 \(B(\cos\beta,-\sin\beta)\)。其中 \(\alpha\) 和 \(\beta\) 是射线与 \(x\) 轴的夹角,不妨令 \(\alpha < \beta\)。
那么,由 \(\overrightarrow{P_jP_i}\) 在扇区内,有
$$ \[\begin{align} \begin{cases} \overrightarrow{OA}\times \overrightarrow{P_jP_i}\le 0\\ \overrightarrow{OB}\times \overrightarrow{P_jP_i}\ge 0 \end{cases} \ \Longrightarrow \begin{cases} \cos\alpha \cdot y_i+\sin\alpha\cdot x_i\le \cos\alpha\cdot y_j+\sin\alpha\cdot x_j\\ \cos\beta \cdot y_i+\sin\beta\cdot x_i\ge \cos\beta\cdot y_j+\sin\beta\cdot x_j \end{cases} \end{align}\] $$
令 \(w_1(P_i)=\cos\alpha\cdot y_i+\sin\alpha\cdot x_i\),以及 \(w_2(P_i)=\cos\beta\cdot y_i+\sin\beta\cdot x_i\),则
\[ \begin{cases} w_1(P_i)\le w_1(P_j)\\ w_2(P_i)\ge w_2(P_j) \end{cases} \]
就转化为了二维数点问题。
离散化后,按其中一维排序,树状数组统计另一维贡献即可。
时间复杂度 \(O(kn\log n)\)。
浮点类型数组的去重:
b.erase(unique(b.begin(), b.end(), [&] (double X, double Y) {
return fabs(X - Y) < eps;
}), b.end());浮点类型数组的 std::lower_bound:
for (int i = 1; i <= n; i++) {
c[i] = lower_bound(b.begin(), b.end(), w[i], [&] (double X, double Y) {
return X < Y - eps;
}) - b.begin() + 1;
}QOJ8542. Add One 2
很牛的一道题,就是官方题解写得太简略了。
首先,我们称题目给的两种操作分别为 "前缀加" 和 ”后缀加“。
称一个全 \(0\) 序列通过任意次前缀加/后缀加得到的序列为 "合法序列"。
注意到,两种操作都是耗费 \(k\) 的代价对长为 \(k\) 的段进行操作,摊到每一个元素上的代价是 \(1\)。
那么,题目等同于让我们在 \(\{y\}\) 上进行若干单点 \(+1\) 操作,使得
- \(\{y\}\) 是 "合法序列"。
- \(\sum\limits_{i=1}^{n} y_i\) 最小。
在此基础上,答案就是 \(\sum\limits_{i=1}^{n}y_i\)。
接着,什么情况下,一个序列 \(\{x\}\) 是 "合法序列"?反向考虑,将 \(\{x\}\) 逐步减为全 \(0\) 序列。
如果 \(\exists i\),\(x_i>x_{i+1}\),那么至少要对 \([1,i]\) 进行 \(x_i-x_{i+1}\) 次前缀减。
同理,如果 \(\exists i\),\(x_i<x_{i+1}\),那么至少要对 \([i+1,n]\) 进行 \(x_{i+1}-x_i\) 次后缀减。
一步一步来,首先,对 \(\{x\}\) 进行如下操作:
- 从头扫一遍,如果 \(\exists i\),\(x_{i}>x_{i+1}\),就对 \([1,i]\) 进行 \(x_i-x_{i+1}\) 次前缀减。\((\alpha)\)。
操作后,\(\{x\}\) 会变成一个非递减序列。继续
- 从头扫一遍,如果 \(\exists i\),\(x_i<x_{i+1}\),就对 \([i+1,n]\) 进行 \(x_{i+1}-x_i\) 次后缀减。\((\beta)\)。
此时,\(\{x\}\) 所有元素将变得相同。
显然,若此时 \(\{x\}\) 中的元素非负,就能断定操作前,\(\{x\}\) 是 "合法序列"。
现在,我们恢复 \(\{x\}\) 到操作前,在头尾添加 \(x_0=x_{n+1}=M\),其中 \(M\) 是一个很大的数字。
进行操作 \((\alpha)\),操作后 \(x_0\) 被减去了 \(\sum\limits_{i=0}^{n}\max(0,x_i-x_{i+1})\)。
再进行操作 \((\beta)\),操作后 \(x_{n+1}\) 被减去了 \(\sum\limits_{i=0}^{n}\max(0, x_{i+1}-x_i)\)。
我们刚刚说过,两遍操作后 \(\{x\}\) 中的元素将变得相同,要让 \(x_0,x_{n+1}\) 非负,则 \[ \begin{cases} x_0-\sum_{i=0}^{n}\max(0,x_i-x_{i+1})\ge 0\\ x_{n+1}-\sum_{i=0}^{n}\max(0,x_{i+1}-x_i)\ge 0 \end{cases} \] 两个不等式相加,移项,代入 \(x_0=x_{n+1}=M\),有 \[ \sum_{i=0}^{n}|x_i-x_{i+1}|\le 2M \] 这就是 \(\{x\}\) 是 "合法序列" 的充要条件了。
现在,题目可以转化为:给定 \(\{y\}\),你可以花费 \(1\) 的代价选择一个 \(y_i\) 加一,问使得以下不等式成立所需的最小花费。 \[ \sum_{i=0}^{n}|y_i-y_{i+1}|\le 2M\tag{*} \] 令 \(F=\sum\limits_{i=0}^{n}|y_i-y_{i+1}|\)。我们每次可以选择一段极长的 \(y_l=y_{l+1}=\ldots=y_r\),满足 \(y_l<y_{l-1}\) 且 \(y_l<y_{r+1}\),将区间 \([l,r]\) 整体 \(+1\)。将 \(\{y\}\) 看成柱状图的话,相当于 "填坑"。
每填一层坑,\(F\) 都会 \(-2\),而我们耗费了 "坑的宽度" 这么多代价。于是,我们的策略肯定是:每次选择宽度尽可能小的坑来填。我们就这样不断填,直到条件 \((*)\) 成立。
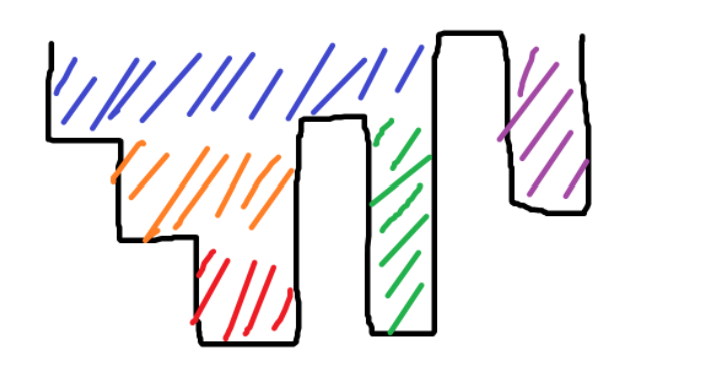
如上图,我们可以预先将 \(\{y\}\) 分成很多小块(以颜色区分)。不难发现,我们既然是贪心拿宽度小的,那我们一定不会发生类似 "红色没填,橙色却先填了的情况"。
于是直接利用单调栈预处理出每个颜色块的宽度(和高度),排序后模拟填的过程即可。
时间复杂度 \(O(n\log n)\)。
QOJ6845. Tax
conclusion. 爆搜是可行的,前提是忽略不在最短路上的边。
做法:
- 从起点跑一遍 bfs,记录到第 \(i\) 个点的最短路径 \(d_i\)。
- 从起点开始 dfs,遍历到一条边时如果 \(d_y\neq d_x+1\) 就跳过,直到遍历完所有可能的路径,代价取最小值。
prove. 按 \(d_i\) 构建分层图。从上至下第 \(j\) 层包含所有 \(d_i=j\) 的点 \(i\)。
只走最短路径,说明每次走的都是第 \(i\) 层到第 \(i+1\) 层的边。
假设第 \(i\) 层有 \(c_i\) 个节点。那么从起点开始,每次往下走一层,走到第 \(i\) 层有 \(\prod\limits_{j\le i} c_j\) 种方案。
找最大路径数,相当于 "将 \(n\) 分成若干正数的和,要怎么分,才能使分出的数的积最大"。
列公式,求导得极值,结论是每层 \(e\) 个点取得最大路径数。取正整数的话就是 \(3\)。
综上,每层向下有 \(3\) 种选择,共 \(\dfrac{n}{3}\) 层,爆搜复杂度是 \(O(\large{3^{\frac{n}{3}}})\)。