【题解】龟速更新的加训日记

vp 多一点还是有好处的。

计划将区域赛前的训练都写在这里。

与以往不同，这篇博客说是题解，实际上只会记录简要的解题思路，用于我日后进行回忆。

如果你无意间点进这里，看不懂是正常的，是写题解的人垃圾而不是你垃圾。

【8.21】NWERC 2023

H. Higher Arithmetic

将一个数拆分成若干正整数，要使得乘积最大，应当先尽可能多地拆成 \(3\)，再尽可能多地拆成 \(2\)。如果最后剩下 \(1\)，就把之前组合出的一个 \(3\) 拆掉，拼成两个 \(2\)。

注：实际上拆分成 \(e\) 最好，只不过 \(3\) 是最接近 \(e\) 的正整数，其次是 \(2\)。

回到这道题，\(\ge 3\) 的肯定直接乘起来，否则想办法凑出多的 \(3\)，其次凑出多的 \(2\)。

J. Jogging Tour

枚举 \(n\) 个点两两之间的 \(n^2\) 条边，最优策略中坐标轴肯定与其中一条边平行。

坐标轴旋转公式（逆时针旋转 \(\theta\)），原坐标 \((x,y)\)，新坐标 \((x',y')\)。 \[\begin{align}\pmatrix{x' \\ y'}=\pmatrix{\cos\theta & \sin\theta\\ -\sin\theta & \cos \theta}\pmatrix{x\\ y}\end{align}\]

之后跑最短哈密顿路径即可。

I. Isolated Island

比较蠢的方法是先建出平面图，再用最小左转法转成对偶图，再从无限面开始 bfs。

这当然是能做的，Link，\(O(n^2\log n)\)，缺点是一大坨。

注意到答案是 \(\texttt {No}\) 当且仅当对偶图是二分图。（相邻点到海边的距离最多相差 \(1\)，按到海边的距离的奇偶性建二分图，这个条件是充要的）二分图意味着没有奇环，因为 "奇 + 偶 = 奇"，如果对偶图有奇环，那么一定存在一个极小的奇环，环内的点度数为奇数。

于是判断输入的 \(n\) 条线段是否有某一个端点只出现了奇数次即可。

G. Galaxy Quest

设在第 \(i\) 条边上我们用了 \(x_i\) 秒来加速。如果我们知道最终走了哪些边，就能转化为线性规划问题 \[ \begin{align} &\min \ 2\sum x_i\\ &\sum x_i + \dfrac{d_i}{x_i}\le t \end{align} \] 拉格朗日乘数法，最终得到 \[ 2\sum x_i=t-\sqrt{t^2-4(\sum \sqrt{d_i})} \] 所以答案越小等同于让 \(\sum \sqrt{d_i}\) 越小。

给每条边赋权 \(\sqrt{d_i}\) 跑 dijkstra 即可，单次 \(O(1)\) 回答询问。

【8.25】2021 ICPC Jinan Regional

C. Optimal Strategy

先考虑所有数出现次数只有偶数的情况，如果一个人拿了最大的，另一个人必须跟着拿，因此可以两两配对。

从小到大考虑每个数，如果新加进一个数 \(x\)，导致 \(x\) 的出现次数变成奇数，先手肯定将 \(x\) 拿走一个，回到刚刚的情况。

对操作序列计数，设 \(f[i]\) 为当前最大的数为 \(i\) 的答案，用隔板法试图将 \(i\) 插进序列 \[ f[i]=f[i-1]\cdot \binom{cnt[i]/2+\sum_{j=1}^{i-1}cnt[j] }{cnt[i] / 2}\cdot cnt[i]! \] 最后乘阶乘表示分配这 \(cnt[i]\) 个 \(i\) 的次序。

L. Strange Series

\[ \begin{align} p&=\dfrac{S}{e}\\ &=\dfrac{1}{e}\sum_{m=0}^{\infty}\dfrac{\sum_{i=0}^{n}a_im^i}{m!}\\ &=\sum_{i=0}^{n}a_i\cdot \dfrac{1}{e}\sum_{m=0}^{\infty}\frac{m^i}{m!} \end{align} \] 令 \(T_i=\dfrac{1}{e}\sum\limits_{m=0}^{\infty}\dfrac{m^i}{m!}\)，我们要对 \(i\in [0,n]\) 求出 \(T_i\)。

对 \(T_i\) 建立 EGF，设 \(F(x)=\sum\limits_{i=0}^{\infty}T_i\dfrac{x^i}{i!}\)。那么 \[ \begin{align} F(x)&=\sum_{i=0}^{\infty}\left(\dfrac{1}{e}\sum_{m=0}^{\infty}\frac{m^i}{m!}\right)\dfrac{x^i}{i!}\\ &=\dfrac{1}{e}\sum_{m=0}^{\infty}\frac{1}{m!}\sum_{i=0}^{\infty}\dfrac{(mx)^i}{i!}\\ &=\dfrac{1}{e}\sum_{m=0}^{\infty}\dfrac{(e^x)^m}{m!}\\ &=e^{e^x-1} \end{align} \] 令 \(G(x)=e^x-1=\sum\limits_{i=1}^{\infty}\dfrac{x^i}{i!}\)。那么 \(T_i=i!\cdot [x^i]e^{G(x)}\)，多项式 \(\text{exp}\) 即可。

B. Monitored Area

对于一个多边形内的监控 \(O\)，以它为原点向多边形的每个顶点做射线，每条射线取极长的在多边形内的部分。极角序相邻的射线与多边形的一条边构成三角形，得到 \(n\) 个三角形，每个监控都这么做，再把所有三角形求并就是答案。

难点是如何正确识别三角形的顶点。我们对每一组极角序相邻的射线考虑，枚举多边形的每条边，对于一条边，如果某一条射线和它没有交点，就排除，否则设交点坐标分别为 \(A,B\)，只用判断线段 \(OA\) 和线段 \(OB\) 是否完全在多边形内部就行。

时间复杂度 \(O(n^4)\)。

M. Coloring Rectangles

每个矩形以其两条对角线为分隔，分出上下左右四个三角形。上和下恰好一个涂黑。左和有恰好一个涂黑，对应了题中的四种情况。用一个变量表示上黑还是下黑，另一个变量表示左黑还是右黑，一种染色情况就能用 \(2n\) 个二元变量来描述。两个三角形如果严格相交，就表示二者不能同时涂黑，2-SAT 即可。

因为要字典序最大，我们可以依次钦定每一个矩形是 \(3,2,1\) 或 \(0\)，最多跑 \(4n\) 遍 2-SAT，最终 \(O(n^3)\)。

两个三角形 \(A,B\) 严格相交（公共面积 \(>0\)），等价于

• \(A\) 中一条边和 \(B\) 中一条边在非三角形端点处规范相交。
• 或者，其中一个三角形的重心严格在另一个三角形内部。

A. Space Station

好难写，占坑。

【8.28】Ucup3-39. Tokyo

K. K-rep Array

数组可以是 \(K\)-rep 当且仅当不存在 \(i,j\) 使得 \(a_i\neq -1,a_j\neq -1,a_i\neq a_j\) 且 \(|i-j|\bmod K=0\)。

令 \(f_d=\sum\limits_{i-j=d}(a_i+1)(a_j+1)(a_i-a_j)^2\)，那么 \(K=i\) 时答案为 \(1\) 当且仅当 \(\forall j,\ i\mid j\)，\(f_j=0\)。

将 \(f_d\) 拆开 \[ \begin{align}f_d&=\sum_{i-j=d}a_i(a_i+1)\cdot (a_j+1)\\&-2\sum_{i-j=d}a_i(a_i+1)\cdot a_j(a_j+1)\\&+\sum_{i-j=d}(a_i+1)\cdot a_j(a_j+1)\end{align} \] 每一项分别计算，差卷积化为和卷积后，用 NTT 求解。

差卷积化和卷积（0-index）： \[\sum_{i-j=d}f(i)g(j)=\sum_{i+(n-j-1)=d+n-1}f(i)g(j)\] 令 \(g_{\text{rev}}(i)=g(n-i-1)\)，化为 \(\sum\limits_{i+j=d+n-1}f(i)g_{\text{rev}}(j)\)。

L. LIS Triangle

如果 \(K=i\) 有解，那么 \(K>i\) 也有解，因为整体加一不影响构成三角形。

\(K=1\) 时无解，\(K=2\) 时一定有解，两种构造如下

\(L=N\) 时要特判。

N. Nice Bouquets

转化题意：找到最小的 \(c\)，通过对树 \(1\sim c\) 操作，使得在所有 \(k\) 天里，每一天三种颜色的花的数量（\(n_R,n_G,n_B\)）都满足 \(n_R\equiv n_G\equiv n_B\pmod {3}\)。

一棵树用长为 \(2k\) 的向量描述：第 \(2i\) 个值表示第 \(i\) 天这棵树对 \(n_R-n_G\pmod {3}\) 的贡献，第 \(2i+1\) 个值表示第 \(i\) 天这棵树对 \(n_G-n_b\pmod {3}\) 的贡献。如此得到 \(n\) 个长为 \(2k\) 的向量构成的向量组 \(\{v_i\}\)。

对第 \(i\) 棵树操作，默认状态 \(1\cdot v_i\)，砍掉即 \(0\cdot v_i\)，加速即 \(2\cdot v_i\)。令 \(V_{\text{init}}=\sum_{i=1}^{n}v_i\pmod{3}\)，目标是选取一组 \(\{a_i\}\) 使得 \[ V_{\text{init}}+\sum_{i=1}^{c} a_iv_i \equiv 0 \pmod{3} \ \ (a_i\in \{0,1,2\}) \] 即向量 \(-V_{\text{init}}\) 是否能被向量组 \(\{v_1,v_2,\ldots,v_c\}\) 线性表出，用线性基求解。

\(GF(3)\) 下的线性基：核心仍然是高斯消元。

基的每一维都是一个向量（当然也可以是三进制数）

GF(3) basis

struct Basis {
	int n;
	vector<vector<int>> p;
	Basis(int _n) : n(_n), p(n) {}
	void insert(vector<int> v) {
		for (int i = n - 1; i >= 0; i--) {
			if (v[i] == 0) {
				continue;
			}
			if (p[i].empty()) {
				p[i] = v;
				return ;
			}
			int fac = v[i] * p[i][i] % 3;
			for (int j = 0; j < n; j++) {
				v[j] = (v[j] - fac * p[i][j] % 3 + 3) % 3;
			}
		}
	}
	bool query(vector<int> v) {
		for (int i = n - 1; i >= 0; i--) {
			if (v[i] == 0) {
				continue;
			}
			if (p[i].empty()) {
				return false;
			}
			int fac = v[i] * p[i][i] % 3;
			for (int j = 0; j < n; j++) {
				v[j] = (v[j] - fac * p[i][j] % 3 + 3) % 3;
			}
		}
		return true;
	}
};

G. Guarding Plan

如果一个哨位已被监视，就可以删去。没被删的哨位构成一条随着 \(x\) 递增，\(y\) 递减的折线（红线），单调栈求出。我们再作出这些哨位的上凸壳（绿线），凸壳内的任意一点均能搞出一个哨位。

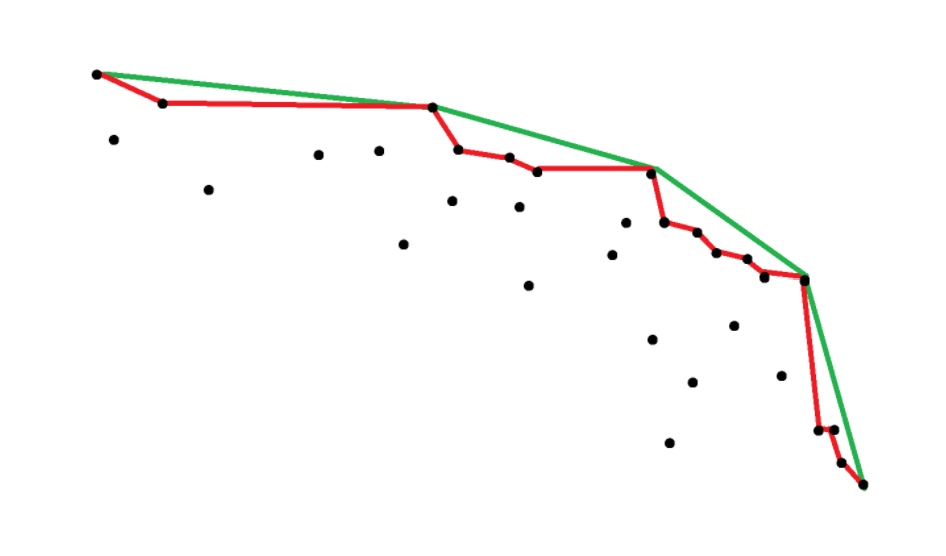
现在，你可以选择在绿线上新建若干点，覆盖掉红线上的一些点，让总点数变少。每段绿线分别考虑，\(dp(i)=(a,b)\) 表示这段绿线对应的红色折线上的前 \(i\) 个点至少能分成 \(a\) 段，且分成 \(a\) 段的前提下至少添加 \(b\) 个新点。

• 当前点选择保留：\(dp(i)=(a,b)\to dp(i+1)=(a+1,b)\)。
• 当前点选择被一个新点覆盖：\(dp(l-1)=(a,b)\to dp(r)=(a+1,b+1)\)。这需要凸包上的一个点完全覆盖 \([l,r]\) 这一段，也就是 \((x_r,y_l)\) 在凸包内。

dp 值是单调的，相同的 \(r\) 转移小的 \(l\) 更优，因此可以单调队列优化。

【8.30】CCPC 2023 Harbin

E. Revenge on My Boss

二分答案，设为 \(T\)。\(T\) 可行 \(\Leftrightarrow\) 重排三元组 \(\{a_i,b_i,c_i\}\) 使得 \(\forall m\in [1,n]\)，\((\sum\limits_{i=1}^{m} a_i+\sum\limits_{i=m}^{n}b_i)\cdot c_m \le T\)。

令 \(d_i=a_i-b_i\)，\(B=\sum\limits_{i=1}^{n}b_i\)，推一下式子，等价的条件是 \[ \sum\limits_{i=1}^{m-1} d_i\le T / c_m-B-a_m \] 不等号右侧均和放置顺序无关，记为 \(e_m\)。现在要重排 \(\{d_i,e_i\}\) 使得 \(\forall m\in [1,n]\)，\(\sum\limits_{i=1}^{m-1}d_i \le e_i\)。

最优策略下，显然先放置 \(d_i\le 0\) 的项，再放置 \(d_i>0\) 的项（其实并不显然，但可以感性理解？）。对于 \(d_i \le 0\) 的项，应当先放 \(e_i\) 较大的，让不等号右侧尽快增大，条件会更宽松；对于 \(d_i>0\) 的项，引入 \(D_i\) 表示 \(d_i\) 的前缀和，条件变成 \(D_i\le d_i+e_i\)，其中 \(d_i+e_i\) 可以看成天花板，我们要想不顶过天花板，策略应当是先放 \(d_i+e_i\) 较小的。

H. Energy Distribution

先忽略 \(e_i\ge 0\) 的条件，拉格朗日乘数法，\(\dfrac{\partial L}{\partial e_k}=0\Longrightarrow \sum\limits_{i\neq k} w_{ik}e_i=\lambda\)，是定值。

枚举子集 \(S\)，钦定子集内的 \(i\) 都满足 \(e_i >0\)，能列出 \(|S|-1\) 个方程，再加上 \(\sum e_i=1\)，就是 \(|S|\) 个，未知数也是 \(|S|\) 个，高斯消元，如果有负数解就舍去。答案对所有子集取 \(\max\)。时间复杂度 \(O(2^nn^3)\)。

C. Karshilov's Matching Problem II

拆贡献，式子可以写成 \(\sum\limits_{i=l}^{r}Sw[\min(r-i+1,z[i])]\)，其中 \(Sw\) 是 \(w\) 的前缀和，\(z[i]\) 是 \(\text{LCP}(T[i,n],S[1,n])\)，可以通过把 \(S\) 和 \(T\) 拼起来跑 Z 函数求得。

找到 \([l,r]\) 里最小的 \(mid\) 满足 \(T[mid,r]\) 是 \(S\) 的一个前缀。\(i<mid\) 的部分 \(\min\) 那项一定取到 \(z[i]\)，因此只用预处理 \(Sw[z[i]]\) 的前缀和；比较困难的是 \(i\ge mid\) 的部分，\(\min\) 那项仍旧有两个可能取值。换一个视角，我们可以对 \(S\) 的每个前缀 \(1\sim k\) 都预处理出 \(f(S[1,k])\)，这样两部分都能 \(O(1)\) 回答。具体的 \[ \begin{align} f(S[1,k])&=\sum_{i=1}^{k}\left(\sum_{S[i-j+1,i] \textbf{是 } S \textbf{ 的一个前缀}} w_j\right)\\ &=\sum_{i=1}^{k}\left(\sum_{j \textbf{ 在 fail 树上是 } i \textbf{ 的祖先} } w_j\right)\\ \end{align} \] 令 \(h[i]=\left(\sum_{j \textbf{ 在 fail 树上是 } i \textbf{ 的祖先} } w_j\right)\)，因为 \(i\) 的祖先集合 \(=\) \(\{i\}\ \cup\) \(\text{link[i]}\) 的祖先集合，所以 \[ h[i]=w_i+h[\text{link}[i]] \] 至于求 \(mid\)，可以在线段树上二分，找 \([l,r]\) 里第一个 \(i+z[i]>r\) 的位置。

【8.31】CCPC Final 2020

E. Game Theory

打表，令 \(k\) 表示 \(1\) 的个数，答案是 \[ \left(\sum_{s_i=1}2i-1\right)-k(k-1) \] 两部分都可以用线段树维护。

J. Permutation Pattern

区间 dp，令 \(f[l][r][i][j]\) 表示只考虑区间 \([l, r]\)，选出的子序列最小值为 \(i\)，最大值为 \(j\) 的答案。对于一个区间，枚举最大值出现的位置 \(m\in [l,r]\)，设 \(\{L\},\{R\}\) 分别表示 \([l,m-1]\) 和 \([m+1,r]\) 选出的符合条件的子序列，那么子序列 \([\{L\},m,\{R\}]\) 满足条件等价于 \(\max\limits_{x\in \{L\}} x< \min\limits_{y\in\{R\}} y\)。

分 () m ..，.. m () 和 .. m .. 转移，前两种表示最大值位于区间端点，第三种可以后缀和加速，总时间复杂度 \(O(n^4)\)。

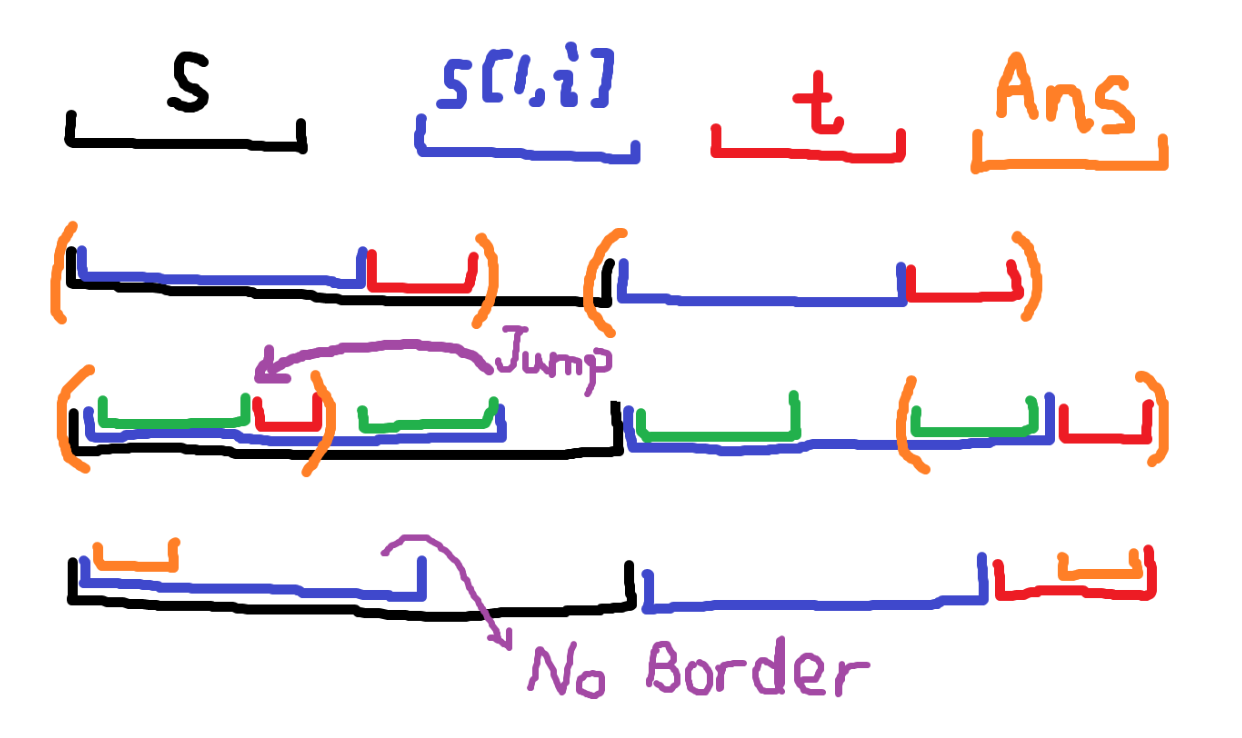
K. Stringology

如下图。

M. 3D Geometry

将四面体的直角顶点平移到原点，三个维度进行缩放，变成标准四面体（\(x,y,z\ge 0,\ x+y+z\le 1\)），变换后的立方体只保留第一卦限的部分，最后计算出的体积交乘一个缩放系数就是答案。

设 \(V(x,y,z)\) 表示区域 \(\{(x',y',z')\mid x'\ge x,\ y'\ge y,\ z'\ge z\}\) 与四面体的体积交，那么总体积交可以拆分成 \[ \begin{align} &+V(x_a,y_a,z_a)\\ &-(V(x_b,y_a,z_a)+V(x_a,y_b,z_a)+V(x_a,y_a,z_b))\\ &+(V(x_b,y_b,z_a)+V(x_b,y_a,z_b)+V(x_a,y_b,z_b))\\ &-V(x_b,y_b,z_b) \end{align} \] 其中 \((x_a,y_a,z_a)\) 和 \((x_b,y_b,z_b)\) 为立方体的对角顶点，\(x/y/z_a<x/y/z_b\)。

【9.2】ZJCPC 2025

C. RDDCCD

任取 \(x=a_{1,1}\)，答案一定是 \(x\) 或 \(\text{rev}(x)\) 的质因数幂的组合。考虑怎么 check 某一个质因数幂 \(p\)。

对每一个矩阵中的 \(y\)，如果 \(y\) 和 \(\text{rev}(y)\) 都不是 \(p\) 的倍数，那 \(p\) 肯定不合法；如果都是，翻不翻无所谓；如果恰有一个是，我们就给这个位置随机赋一个 \(v\)，接着将 \(y\) 所处的两条对角线异或上 \(v\)。如此，每次更改一条对角线，我们就能快速计算当前相比初始状态被翻的格子对应 \(v\) 的异或和 \(\text{cur}\)。再令 \(\text{need}\) 表示使 \(p\) 合法应该翻的格子对应的 \(v\) 的异或和，比较 \(\text{need}\) 是否等于 \(\text{cur}\) 即可。单次 check \(O(n^2+q)\)。

M. Master of Both VII

问所有 \(i\in [3,n-1]\) 的 \((1,i)\)，记为 \(d_i\)。如果 \(d_i=0\)，直接计入答案。

一条边 \((x,y)\) 与 \((1,i)\) 在非端点处相交的充要条件是 \(1<x<i<y\le n\)。考虑 \(d_i-d_{i-1}\) 的意义，是 "以 \(i-1\) 为起点的边数 \(-\) 以 \(i\) 为终点的边数"。又因为任何一个三角剖分中形如 \((i-1,y),\ y>i\) 的边和形如 \((x,i),\ x<i-1\) 的边不可能同时存在，所以上述差值中的两项必有一个为 \(0\)。

• 若 \(d_i-d_{i-1} >0\)，说明有 \(d_i-d_{i-1}\) 条边以 \(i-1\) 为起点。
• 若 \(d_i-d_{i-1}<0\)，说明有 \(d_{i-1}-d_i\) 条边以 \(i\) 为终点。

用一个栈存储还没配对的边的起点，遇到一个终点时就弹栈配对。

【9.4】Ucup3-24. Poland

L. Looping RPS

将 \(s_i^{\infty}\) 插入 trie，三个人有贡献当且仅当它们在同一个点的三个不同子树内。考虑枚举每个点作为 LCA 计算贡献，当然我们不用真的建出 trie，只用从根开始 dfs，维护当前路径是多少个不同串的前缀。

实践证明，只要将所有 \(s_i\) 保留最小整周期并去重，就能跑得很快，复杂度我也不会证。

D. Diminishing Fractions

分母不超过 \(M=\text{lcm}\{1,2,\ldots,n\}\)，答案下界是 \(\dfrac{1}{M}\)，尝试构造。因为 \(M=\prod p^{k_p}\)，其中 \(k_p\) 是最大的满足 \(p^{k_p}\le n\) 的幂次，我们可以直接选择这些不超过 \(n\) 的最高质数次幂作为分母，记为 \(\{d_1,d_2,\ldots,d_m\}\)。现在需要寻找对应的分子 \(\{a_1,a_2,\ldots,a_m\}\)，使得： \[ \sum_{i=1}^{m}\dfrac{a_i}{d_i}=\dfrac{1}{M} \] 这个不好构造，但题目允许我们最后减去一个形如 \(K/1\) 的整数 \(K\)，所以可以写成 \[ \sum_{i=1}^{m}\dfrac{a_i}{d_i}=K+\dfrac{1}{M}\ \longrightarrow\ \sum_{i=1}^{m}a_i\cdot \dfrac{M}{d_i}\equiv 1\pmod{M} \] 这个式子可以拆成 \(m\) 个 \(\bmod d_i\) 的同余式，且 \(\gcd(M/d_i,d_i)=1\)，存在逆元，因此直接能 exgcd 求出 \(a_i\)。那么 \(K\) 是多少？直接 double 加起来取整数部分。

对于多组数据，离线，按 \(n\) 从小到大回答询问，想办法更新贡献就行，有点复杂但总能改出来。时间复杂度 \(O(n\pi (n)+\pi(n)\log n)\)。

【9.5】EC Final 2024

K. Exploration Boundary

一个点集成为边界时，整张图被划分成三个部分，因为 Dijkstra 按最短路递增的顺序访问，边界上和边界外点的距离必然不小于和边界内点的距离。因此将边界看成一堵墙，从起点 bfs，若某个时刻没有点可遍历，且已遍历的点包含了一个题目给出的边界，这个边界就是合法的。

现在题目给出多个边界，这些边界包含的内部的点必然是包含关系，访问顺序唯一。我们可以初始把所有边界都看成墙，每遍历完一个边界，就将这个边界拆掉并加进队列继续 bfs，以此类推（匹配边界可以直接 std::set）。注意一个点可能是多个边界的一部分，所以要按拓扑排序减入度的方法处理。考虑赋边权，设 \(x\) 在我们得到的拓扑序中排第 \(h_x\) 个，那么一条边赋 \(|h_x-h_y|\) 是理想的，既能保证出队顺序，也能满足从起点出发最短路互不相同的限制。

L. Shiori

操作一和三都是线段树标准操作。操作二分两步：先找到 mex，再区间加。我们主要看怎么找 mex。线段树维护区间最小值 \(mn\)，对于一次询问，只有完全被 \([l, r]\) 包含的区间的 \(mn\) 有用。我们先找到一个极小的不交区间集合 \(\{S\}\)，区间并恰好是 \([l,r]\)，事实上这就是线段树查询时访问的区间，递归一遍即可找出。接着将 \(\{S\}\) 塞进优先队列，规则是 \(mn\) 小的靠前。现在，我们尝试逐步找到 \(x=0,1,2,\ldots\)，第一个找不到的就是 mex。

首先，取出优先队列顶的 \([u,v]\)，如果对应的 \(mn>x\)，就找到了；否则 \(x\leftarrow x+1\)，并递归遍历 \([u,v]\) 的子树，将 \(mn>x\) 的次一级子区间塞进优先队列。单次操作，这样的子区间有 \(\log\) 个，时间复杂度均摊 \(O(n\log^2 n)\)。

【9.6】Ucup3-40. Potyczki

打完一看怎么是波兰语题解，看的太费劲了，开了翻译都看不太懂，网上也没有别人写的题解，看别人代码也猜不出做法，有一种无力感，先白兰了。

【9.7】Asia EC Online 2025 (I)

C. Canvas Painting

贪心，把线段按右端点从小到大排序，右端点相同按左端点从小到大排序。然后找到 \([l, r - 1]\) 里第一个未被染色的 \(p\)，让 \(a_p = a_r\)，并将 \(p\) 标记为已经染色。实际上每次只用把 \(ans\) 减一，而找 \(p\) 的过程可以动态开点权值线段树或者 set 维护区间并再 lower_bound。

J. Moving on the Plane

将曼哈顿距离转成切比雪夫距离，那么 "任意两点曼哈顿距离 \(\le k\)" 等价于 "\(x\) 轴和 \(y\) 轴的极差都 \(\le k\)"，且每一步在切氏距离下等同于 \(x\) 方向 \(\pm 1\)，或 \(y\) 方向 \(\pm 1\)，两个轴的答案可以乘起来，我们只用研究一维的情况。

即，数轴上 \(n\) 个点，每次走一格，最后极差 \(\le k\) 的方案数。枚举区间左端点 \(L\)，点只能在 \([L,L+k]\) 移动，再枚举每个点在哪停下，组合数算方案数（向 \(x\) 轴正方向走看成 \(1\)，负方向走看成 \(0\)，插板法），每个点的答案可以乘起来。

为避免算重，要钦定最后 \(L\) 上有一个点，故容斥减去 \([L+1,L+k]\) 的方案数。时间复杂度 \(O(nmk)\)。

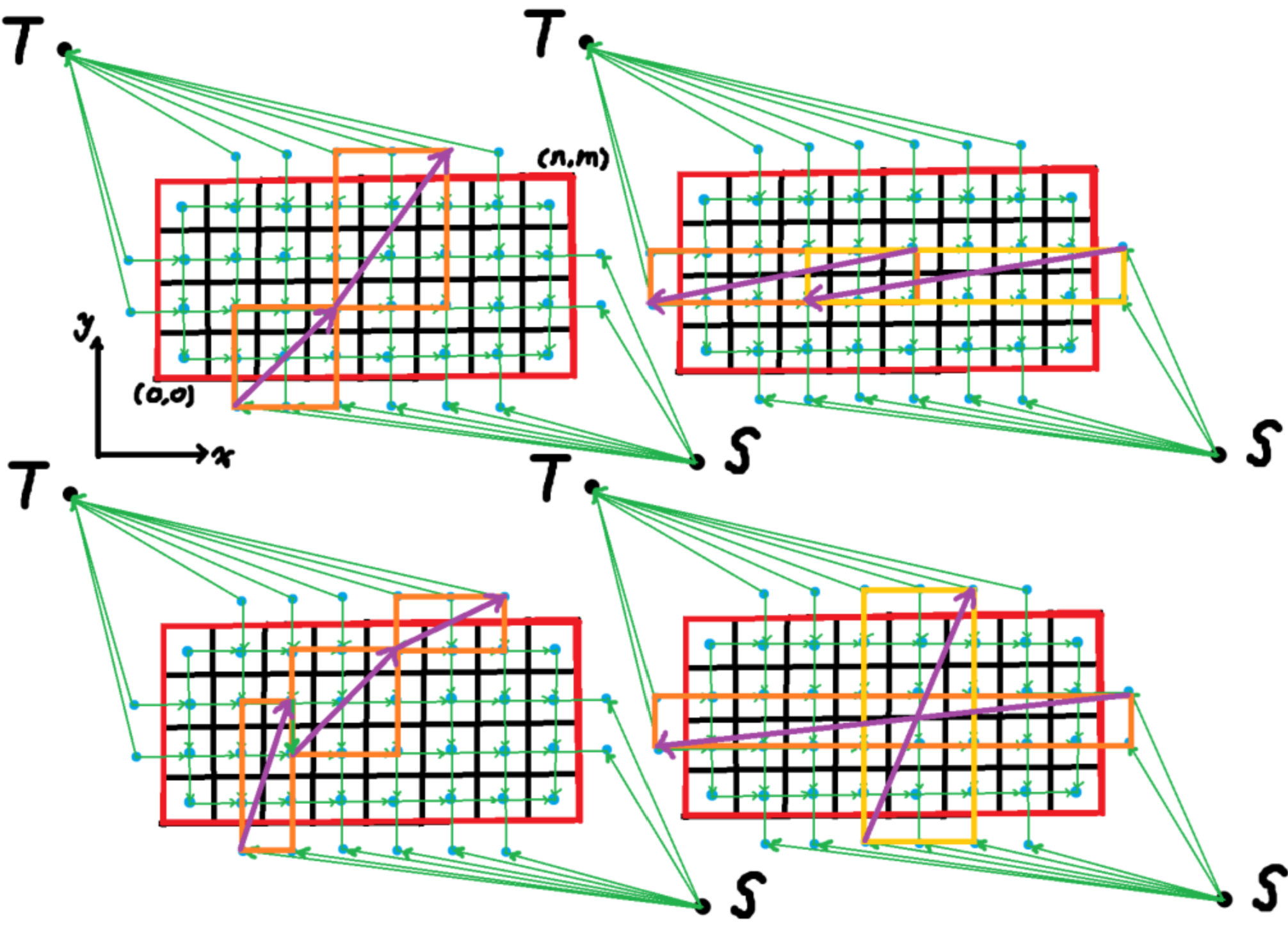
H. Walk

网络流，建模如下。对于一个矩形，左下指向右上的边容量为 \(a\)，右上指向左下的边容量为 \(b\)。

【9.9】CCPC 2024 Zhengzhou

D. Guessing Game

对每一组 \((a_i,b_i)\)，连 \((L_{a_i},R_{b_i})\)，建立二分图。题目可以转化为，从左部点中取走所有度数为 \(1\) 的点，加进 Alice 的答案；再从右部点中取走所有度数为 \(1\) 的点，加进 Bob 的答案。点被取走后，相连的边一并消失，重复上述流程直到图中没有点度数为 \(1\)。对每个连通分量考虑：

• 如果是树，那么可以一直取点直到剩一个孤点，容易说明这个孤点就是树的中心。知道树的直径的奇偶性以及端点的颜色，分情况可以讨论出树的中心的颜色。（"颜色" 即位于左部点还是右部点）
• 如果有环，环上的点度数一定不会是 \(1\)，给个标记。环外被分为多个以被标记的点为根的有根树，除了根外的所有点都能被取走。注意两个环中间的链也要被标记。

考虑加边的过程。对于新加的边 \((x,y)\)，设 \(u,v\) 分别表示 \(x,y\) 所在的连通块。

• \(u=v\)。若 \(u\) 是树，离线按加边顺序建出生成树，那么相当于减去 \(x\to y\) 这一段树上路径的贡献，然后标记 \(x\) 和 \(y\) 的 LCA。若 \(u\) 是环，则从第一次成环标记的 LCA（设为 \(p\)） 开始，减去 \(p,x,y\) 三点间路径的贡献，并更新 \(p\) 为 \(p,x,y\) 三点的 LCA。每次我们可以暴跳，只要打个标记，每个点至多遍历一次。

• \(u\neq v\)。若 \(u,v\) 都是树，合并后维护新连通块的直径，从 \(u,v\) 两条直径的四个点中选出；若 \(u,v\) 一环一树，把树的中心的贡献加回来；若 \(u,v\) 都是环，离线后依然变成减去一段路径的贡献。

【9.12】2024 ICPC Kunming Regional

I. Items

生成函数列出来，相当于求 \([x^m]f(x)^n>0\)。令 \(B=\left\lfloor\frac{m}{n}\right\rfloor\)，\(w_i\leftarrow w_i-B\)，\(m\leftarrow m-nB\)，这一步将 \(m\) 的值域调整到了 \([0,n]\)。但此时 \(w_i\in [-B,n-B]\)，直接多项式快速幂行不通。

一个相当强的观察：如果存在一个方案使得能取到 \(m\)，那么就一定可以调整取物品的顺序，让背包的大小一直保持在 \([0,n]\)。这意味着，多项式每乘一次，只截取 \(x^{-n}\sim x^n\) 就足够。利用类似整数快速幂的方式倍增，\(O(n\log^2 n)\)。

B. Brackets

对每个区间来说，将其化简后必须是一段左括号或者一段右括号，这样才有可能匹配。于是，我们只要想办法高效地化简所有区间，并给每个剩下左括号的区间一个哈希值。至于剩下右括号的区间，将序列翻转再做一遍就好。

从左向右扫，维护一个括号栈，以及栈内元素的哈希值，以及一个标记 ok[i]，表示 \(i\) 可以成为一个合法括号序列的左端点。遇到左括号，标记合法并入栈；遇到右括号，如果匹配，弹栈，注意到与之匹配的左括号右侧不会有新的合法左端点，于是取消这一段的合法标记。如果不匹配，直接将栈清空，并将之前给的合法标记全部撤销。每扫到一个区间的右端点，如果左端点合法，就记录哈希值。

注意一个区间化简后为空集的情况，设有 \(x\) 个这样的区间，贡献就是 \(\left\lfloor\frac{x}{2}\right\rfloor\)。

D. Dolls

如果一段区间可以合成一个套娃，其任意一个子区间也可以。如果一段区间不能合成一个套娃，那所有包含该区间的区间都不行。即，固定左端点时，右端点能二分。对于一段要 check 的区间，先离散化。在最优策略下，若有两个相邻套娃可以紧密合并，就合并它们。模拟这个过程，检查一段长为 \(m\) 的区间是 \(O(m\log m)\)，反推二分初始区间长度的和是 \(k\) 的情况下，是 \(O(k\log^2 k)\)。要让 \(k=O(n)\)，每次二分的右端点不应选取 \(n\)，而是通过倍增来确定。

【9.13】2024 ICPC Shenyang Regional

D. Dot Product Game

下标 \(i, j\) 能操作当且仅当 \((a_i-a_j)(b_i-b_j)<0\)，令 \(\{c\}\) 表示按 \(\{a\}\) 顺序排列的 \(\{b\}\) 数组，那么每次操作定会让 \(\{c\}\) 的逆序对数减少。

对于任意 \(1\sim n\) 的排列，交换任意下标不同的两个数，逆序对数的奇偶性一定会改变。

游戏结束时逆序对数为 \(0\)，于是答案取决于 \(\{c\}\) 的逆序对数的奇偶性。对于一次修改，将 \([l, r]\) 循环左移一次等价于进行了 \(r-l\) 次交换，检查 \(d(r-l)\) 的奇偶性即可，和操作 \(\{a\}\) 还是 \(\{b\}\) 一点关系都没有。

I. Growing Tree

比较考验实现方式的题目。从底向上考虑，如果存在一个节点往下延伸的两条链权值相同，马上砍掉其中一条是最优的。也不可能两条全砍掉，因为这样不如把其中一条放到父亲节点决策。因为最多修改 \(n\) 条边，递归次数是 \(2^n\) 级别，只要实现的不是特别差，爆搜都能过，细节不赘述了。

H. Guide Map

这题真的只有 median 吗？等 C12AK 教我。

【9.15】北京市赛 2025

I. 最小LCM

令 \(d=\gcd(a+x,b+y)\)，那么 \(\text{lcm}(a+x,b+y)=\dfrac{(a+x)(b+y)}{d}\)。当 \(d\) 确定时，\(a+x\) 肯定是取到最小的 \(\ge a\) 的 \(d\) 的倍数最优，\(b+y\) 同理，于是 \[ \begin{cases} x=d \times \left(\left\lfloor \frac{a-1}{d} \right\rfloor + 1\right)-a\\ y=d \times \left(\left\lfloor \frac{b-1}{d} \right\rfloor + 1\right)-b \end{cases} \] 当且仅当 \(0\le x,y\le k\) 时计入答案。注意到当 \(d\) 在一个区间 \([l,r]\) 连续取值时，\(\left\lfloor \frac{a-1}{d} \right\rfloor\) 不变，且取 \(d=l\) 最优，数论分块即可。corner case 是 \(d=a\) 以及 \(d=b\)。时间复杂度 \(O(\sqrt{a}+\sqrt{b})\)。

J. 四舍五入

满足 \(f(x,k)=y\) 的 \(x\)，位于闭区间 \(\left[y-\left\lfloor \frac{k}{2}\right\rfloor,y+\left\lfloor \frac{k-1}{2}\right\rfloor\right]\) 之内。首先，\(y\) 一定是 \(k\) 的倍数。对于一个 \(y\) 来说，每个 \(k\) 都对应一个区间，这 \(m\) 个区间的并表示了一步之内能达 \(y\) 的 \(x\) 的取值范围，设为 \([l_{y,0},r_{y,0}]\)。

进一步，将 \([l_{y,i},r_{y,i}]\) 定义成在 \(2^i\) 步之内能达 \(y\) 的 \(x\) 的取值范围，有

• \(\large l_{y,i}=\min_{u\in [l_{y,i-1},r_{y,i-1}]}l_{u,i-1}\)。
• \(\large r_{y,i}=\max_{u\in [l_{y,i-1},r_{y,i-1}]}r_{u,i-1}\)。

利用 ST 表维护 \(l_{y,i}\) 和 \(r_{y,i}\)，查询时只需要对第一维进行倍增，时间复杂度 \(O(n\log^2 n+q\log n)\)。

K. 最小生成树

一条边 \((x,y,w)\) 在图上的至少一棵最小生成树中 \(\Longleftrightarrow\) 只考虑边权 \(<w\) 的边时，\(x\) 和 \(y\) 在不同的连通分量。

意味着，按边权从小到大加边，当添加一条边权为 \(w\) 的边时，两个端点只能从不同的连通块中寻找。

令 \(f_{k,n}\) 表示边权 \(\in [1,k]\)，点数为 \(n\) 的连通图数量。\(g_{k,n}\) 则表示不一定连通。一个很好的性质是如果令 \(F_k\) 表示 \(f_{k}\) 的 EGF，\(G_k\) 表示 \(g_k\) 的 EGF，那么 \(G_k=\text{exp}(F_k)\)。求出 \(G_k\) 后只需要一次多项式 \(\text{ln}\) 就能求出 \(F_k\)。

设 \(1\) 所在的连通块为 \(A\)，其余点（不一定连通）为 \(B\)。枚举 \(A\) 的大小，列出式子： \[ \large g_{k,n} = \sum_{i=1}^{n} \underbrace{\binom{n-1}{i-1}}_{\text{选出 A 除了 1 之外的 i - 1 个点}} \cdot \underbrace{f_{k-1,i}}_{\text{ A要连通}} \cdot \underbrace{g_{k,n-i}}_{\text{B不一定连通}} \cdot \underbrace{2^{i(n-i)}}_{\text{连接 A, B 的边}} \] 这和半在线卷积的式子很像，尝试往半在线卷积的标准形式进行修改。

\[i\cdot (n-i)=\binom{n}{2}-\binom{i}{2}-\binom{n-i}{2}\]

代入，整理 \[ \large \underbrace{\frac{g_n}{2^{\binom{n}{2}}n!}}_{H_n}=\frac{1}{n}\sum \underbrace{\frac{f_i}{2^\binom{i}{2}(i-1)!}}_{I_{i}}\underbrace{\frac{g_{n-i}}{2^{\binom{n-i}{2}}(n-i)!}}_{H_{n-i}} \]

也就是 \(nH_n=I_iH_{n-i}\)，相比标准形式多了个 \(n\)，联想到 \((x^n)'=nx^{n-1}\)，故取生成函数 \[ \sum_{n\ge 1}nH_n x^n=x\cdot\sum_{n\ge 1}nH_n x^{n-1}=\sum_{n\ge 1}\sum_{i=1}^{n}I_iH_{n-i} x^n \] 即 \(xH'(x)=I(x)H(x)\)，进一步 \[ \begin{align} \frac{H'(x)}{H(x)}&=\frac{I(x)}{x}\\ \int\frac{H'(x)}{H(x)}&=\ln H(x)=\int \frac{I(x)}{x}\\ H(x)&=\text{exp} \left(\int \frac{I(x)}{x}\right) \end{align} \] 这样就跑通了整个 \(f_{k-1,n}\to g_{k,n}\to f_{k,n}\) 的流程，重复 \(k\) 次，时间复杂度 \(O(kn\log n)\)。

【9.16】2020 ICPC Shenyang Regional

I. Rise of Shadows

一天分为 \(HM\) 个单位。分针速度 \(H\) 单位每分钟；时针速度 \(1\) 单位每分钟。相对速度 \(H-1\)，相当于求有多少个 \(t\in [0,HM-1]\) 满足 \[ \begin{align} (H-1)t\ \bmod{(HM)}\le A \quad\textbf{ 或 }\quad (H-1)t\ \bmod{(HM)}\ge HM-A \end{align} \]

对于 \(f(x)=ax\bmod b\)，令 \(g=\gcd(a,b)\)，那么 \(f(x)\) 有 \(\frac{b}{g}\) 个可能取值，分别为 \(\{0,g,2g,3g,\ldots,(\frac{b}{g}-1)g\}\)。同时，\(\frac{b}{g}\) 也是 \(f(x)\) 的最小正周期。

令 \(G=\gcd(H-1,HM)\)，\(t'\in [0,\frac{HM}{G}]\)，式子改写成 \[ \begin{align} \frac{(H-1)t'}{G}\ \bmod{\frac{HM}{G}}\le \frac{A}{G} \quad\textbf{ 或 }\quad \frac{(H-1)t'}{G}\ \bmod{\frac{HM}{G}}\ge \frac{HM-A}{G} \end{align} \] 令 \(k'=\frac{H-1}{G}\)，\(n'=\frac{HM}{G}\)，\(\gcd(k',n')=1\)，\(g(t')=k't'\bmod n'\) 构成双射（且是置换），答案就是 \([0,n'-1]\) 中满足 \(x\le \frac{A}{G}\) 或 \(x\ge \frac{HM-A}{G}\) 的 \(x\) 的数量，即 \(2\left\lfloor\frac{A}{G}\right\rfloor+1\)，再乘上周期数 \(G\) 就是答案。

C. Mean Streets of Gadgetzan

每个子句中至多一个正文字的 SAT 问题称为 Horn-SAT，是能线性解决的。对于蕴含式 \(x_1,x_2,\cdots,x_k\to y\)，从 \(x_1,x_2,\cdots,x_k\) 向 \(y\) 连边，对于非蕴含式，直接扔进 queue 里，拓扑排序。维护 \(\text{ans}[x]=0/1/{-1}\) 表示 \(x\) 尚不确定，确定为正，确定为负，看看有没有冲突就行。

E. Knights of the Frozen Throne

令 \(t_i^{(j)}\) 表示第 \(i\) 个玩家的第 \(j\) 发请求。合法的 \(X\) 取值只有 \[ \{t_i^{(j)}-t_{i}^{(j-1)}+1\mid 1\le i\le m,\ 2\le j\le k_i\} \] 扫描线，按 \(X\) 从小到大维护贡献。CPU 部分，只需要 map 维护所有需要 load 的时刻；内存部分，当 \(X\) 逐步增大的时候，有些区间的贡献从 \(X\) 变为 \(t_i^{(j)}-t_i^{(j-1)}\)，变了的部分直接累加，再维护仍是 \(X\) 的区间的个数即可。

L. Forged in the Barrens

考虑朴素的 dp，令 \(f[i][k][s=0/1/2]\) 表示考虑前 \(i\) 个数，已经分成了完整的 \(k\) 段，当前段什么都没选 \((s=0)\)，只选了最小值 \((s=1)\)，只选了最大值 \((s=2)\) 的答案，枚举当前 \(a_i\) 作为当前段的极值进行转移。

注意到以 \(k\) 为自变量，\(f[i][k]\) 具有凸性，可以利用分治配合 \((\max,+)\) 卷积进行合并。具体的，令 \(g[p][l=0/1/2][r=0/1/2][k]\) 表示线段树上节点 \(p\) 对应的区间，已经分成了完整的 \(k\) 段，左端点/右端点作为新段非极值/最小值/最大值的答案，那么 \[ g[p][l][r][k]=\max\begin{cases} g[2 \cdot p][l][r][k]\\ g[2\cdot p+1][l][r][k]\\ \max\limits_{s_1,s_2\in[0,2]}\left(\max\limits_{k=i+j} (g[2\cdot p][s_1][0][i]+g[2\cdot p+1][0][s_2][j])\right)\\ \max\limits_{s_1,s_2\in[0,2]}\left(\max\limits_{k=i+j+1} (g[2\cdot p][s_1][1][i]+g[2\cdot p+1][2][s_2][j])\right)\\ \max\limits_{s_1,s_2\in[0,2]}\left(\max\limits_{k=i+j+1} (g[2\cdot p][s_1][2][i]+g[2\cdot p+1][1][s_2][j])\right) \end{cases} \] 对于凸序列 \(a,b\)，单次 \((\max,+)\) 卷积的复杂度是 \(O(|a|+|b|)\)，故总复杂度为 \(O(n\log^2 n)\)。

【9.18】Ucup2-2. SPb

D. Bishops

显然棋盘可以分成两部分，两部分答案可加，互不干扰。将主对角线看成左部点，副对角线看成右部点，构建二分图，我们需要求出一个最大匹配。注意到每个左部点 \(i\) 向右部点的连边都是一段区间 \([L_i,R_i]\)，考虑贪心：将三元组 \((i,L_i,R_i)\) 按 \(R_i\) 升序排序，每次二分出第一个 \(\ge L_i\) 的未被匹配的右部点进行匹配。

一个技巧是将左部点编号为 \(s=i+j\)，右部点编号为 \(t=i-j\)，这样构造方案的时候容易还原。

G. Graph Cuts

没什么好说的，记录一个坑。

bitset<5> a;
a[0] = 1;
a[2] = 1;
auto b = a.flip();
cout << a << "\n";
cout << b << "\n";

第五行，输出的是 11010 而不是 00101。a.flip() 调用的时候直接改变了 \(a\) 本身，而并非创建了一个副本。

C. Many Many Cycles

conclusion. 任意求出一棵生成森林，只用考虑至多包含两条非树边的环。

我们将仅含一条非树边的环称作基本环，先累计基本环答案，再 \(O(m^2)\) 枚举两条非树边，设各自形成的两个基本环分别为 \(a,b\)，容斥一下，新环长 \(|c|=|a\oplus b|=|a|+|b|-2|a\cap b|\)，又 \(\gcd(|a|,|b|,|c|)=\gcd(|a|,|b|,2|a\cap b|)\)，我们只用求 \(a,b\) 在生成树上的交集长度，见树链求交。

同样的，图上任意一个环 \(p\) 都能表示成多个基本环的异或。观察 \(p=a\oplus b\oplus c\)，推一下有 \(|p|=|a|+|b|+|c|-2|b\cap c|-2|a\cap(b\oplus c)|\)。最后一项能拆成 \((a\cap b)\oplus (a\cap c)\)，即两个基本环交集的线性组合。进一步，任意 \(|p|\) 都能用基本环和两个基本环的交集线性表出，得证。

出于神秘的原因，使用随机的生成树相比使用 dfs 树会让程序效率大幅下降。

【9.20】CCPC Online 2025

找不到题解，剩下的题等题解出了再补。

C. 造桥与砍树

令生成树点集为 \(S\)，初始 \(S=\{1\}\)，之后尝试不断扩大 \(S\)。对一个点 \(u\)，优先找 \((a_u+a_v)\bmod k\) 最小的 \(v\)。对 \(S\) 里的每个点 \(u\) 都维护一个 \(v\)，放进优先队列中，每次取最小的加进 \(S\)，并更新 \(v\) 的候选值。本质上就是以 \((a_u+a_v)\bmod k\) 作为权值跑了一遍 prim，并用 set 或其它数据结构加速这个过程。

【9.22】XVI Open Cup. Moscow

E. Super Backpack

题意可以转化为给定 \(n\) 个长度不超过 \(5\) 的序列，求它们的 \((\max,+)\) 卷积。如果是凸序列，容易在 \(O(n\log n)\) 内分治合并，可惜并不凸。

conclusion. 设最终答案序列为 \(d\)，按下标\(\bmod 12\) 分组，分出的 \(12\) 个新子序列都是凸的。

prove. 即证 \(2\cdot d[i+12]\ge d[i]+d[i+24]\) 对任意 \(i\) 成立。假设我们有下标和分别为 \(i\) 和 \(i+24\) 的最优方案 \(S_k=\{c_1,c_2,\ldots, c_n\}\) 和 \(S_{k+24}=\{c_1',c_2',\ldots,c_n'\}\)，其中 \(\sum (c_i'-c_i)=24\)。值域为 \([1,5]\)，即 \((c_i'-c_i)\in [-4,4]\)。注意到（根本注意不到），任何一个由 \(\{-4, -3, \ldots, 3, 4\}\) 中的整数构成的、总和为 \(24\) 的多重集，都可以被划分成两个子集，每个子集的和均为 \(12\)。因此，我们一定能构造出两个总价值之和为 \(d[i]+d[i+24]\)，下标和均为 \(i+12\) 的可行解（注意不一定最优解）。假设这两个子集的价值分别为 \(v_a,v_b\)，因为最优解一定不小于任何一个可行解，有 \(d[i+12]\ge v_a\) 和 \(d[i+12]\ge v_b\)，两式相加，\(2\cdot d[i+12]\ge v_a+v_b=d[i]+d[i+24]\)，得证。

分治合并时，下标\(\bmod 12=k\) 的组，答案是所有 \(k=i+j\) 的组的 \((\max,+)\) 卷积的 \(\max\)。虽然两个上凸序列的 \(\max\) 不一定上凸，但合并完一定是凸的。时间复杂度 \(O(12^2\cdot n\log n)\)。

【9.23】EC Final 2023

I. Balance

首先，同一边双内 \(a_i\) 必须相同，否则一个环会贡献两倍极差。缩边双，得到一棵树，所有 \(a_i\) 相同的连通块，也必定是从小到大像一条链一样排列。设 \(a_i\) 有 \(k\) 种取值，分别记为 \(c_1,c_2,\ldots,c_k\)，我们要找一条路径，路径上按次序有 \(k-1\) 条特殊边，第 \(i\) 条边分隔了 \(c_i\) 和 \(c_{i+1}\)。

显然，对于一条特殊边 \((u,v)\)，其中一侧的连通块大小必定是 \(c_i\) 的一个前缀。要注意，特殊边是有方向的，例如钦定边 \((u,v)\) 表示 \(v\) 所在连通块的大小，一条合法路径顺次经过的特殊边方向必须相同。一个巧妙的转化是：我们只用找同方向特殊边最多的路径，因为上界就是 \(k-1\)。换根 dp 即可，时间复杂度 \(O(n)\)。

【9.25】EC Final 2021