【游记】2024 CCPC 网络预选赛

UESTC_EndlessEmbrace 第一场正式的比赛。

快到九点才起床，本来昨晚和同样晕车的 kkaaxxrrdxing4c 商量好了一起做地铁去，但起床一刷消息发现被鸽了，只好重新买上了九点半的车票，赶忙跑去东门把模板印了。

很困，昨晚临时补了一些板子，两点才睡。车上很颠，没睡着，意料之中。

12点整，PTA 准时开崩。以前只是有所耳闻，这下身临其境了。

队友和我上去打了点板子，期间刷新出了一道签 L，马上秒了（伏笔），继续敲板子。

大概 44min 终于能交题了，交，WA，字符串读的 0-index 写的 1-index，气晕了，47minL2A。

接着签 B，WA。wbc 签 K，63minK1A，随后发现我少了个特判，加上过了，64minB2A。

队友开 D，我开其它的，两个队友都是 dp 糕手，讨论出了一个区间 dp，115minD1A。

PTA 发了延时通知，延了 1h，很难评价。

看榜 UESTC_PenaltyAutomaton 过了不到 10 个队过的 C，大为震撼。

于是看了 C，跟 wp 说了一个贪心，不知道对不对就上去写了，WA，换了一个贪心策略又 WA 了两发，耻辱换题。按榜看了 J，写了两发线性基，还是 WA，红了。

这期间队友一直在攻 E，两个多小时终于找对了方向，283minE2A。

冷静了一下，改了一下线性基的逻辑，终于 287minJ3A。

时间不多了，一起看 I，wp 很快就会 dp 了，就让他上去写，我在研究 C。

跟队友简单说了一下我的做法，觉得很对啊，就打印了一下肉眼查错，后来发现假完了。

最后半小时 I 题狂 T，一起帮着 wp 卡常，可惜的是直到比赛结束也没卡过。

6 题 Rank360/9 收尾，有点沮丧。赛后发现 C，G，I 都不应该丢，但马后炮也意义不大，只能希望下周 ICPC 打得好一点。

FunFact：赛后把 I 题 clone 下来开大了时限把赛时代码交了上去，1952msAccepted，赛时时限是 1s。

---

A. 军训 I

可以预见的是合法的状态数很少。

实际上可以证明 \(k > 13\) 时无解：把所有人移到一个角，这些人在这个角最多只有 \(2\) 种方案，移到一个角之后向另外三个角移动一共 \(2\cdot 4=8\) 种。四个方向单移动一次共 \(4\) 种，再加上原状态 \(1\) 种共 \(13\) 种。

对 \(k\in [1,13]\) 打表发现 \(k=8,10,12\) 时无解，同时还能很快打出 \(\min(n,m)<3\) 的情况进行特判。

打表程序

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff




//-------------- templates above --------------



void solve() {
	int n, m;
	cin >> n >> m;
	for (int k = 1; k <= 20; k++) {
		vector a(n, vector<int>(m));

		auto do_L = [&] () {
			vector b = a;
			b.assign(n, vector<int>(m, 0));
			for (int i = 0; i < n; i++) {
				int cnt = 0;
				for (int j = 0; j < m; j++) {
					cnt += a[i][j];
				}
				for (int j = 0; j < cnt; j++) {
					b[i][j] = 1;
				}
			}
			a = b;
		};
		auto do_R = [&] () {
			vector b = a;
			b.assign(n, vector<int>(m, 0));
			for (int i = 0; i < n; i++) {
				int cnt = 0;
				for (int j = 0; j < m; j++) {
					cnt += a[i][j];
				}
				for (int j = m - 1; j >= m - cnt; j--) {
					b[i][j] = 1;
				}
			}
			a = b;
		};
		auto do_U = [&] () {
			vector b = a;
			b.assign(n, vector<int>(m, 0));
			for (int j = 0; j < m; j++) {
				int cnt = 0;
				for (int i = 0; i < n; i++) {
					cnt += a[i][j];
				}
				for (int i = 0; i < cnt; i++) {
					b[i][j] = 1;
				}
			}
			a = b;
		};
		auto do_D = [&] () {
			vector b = a;
			b.assign(n, vector<int>(m, 0));
			for (int j = 0; j < m; j++) {
				int cnt = 0;
				for (int i = 0; i < n; i++) {
					cnt += a[i][j];
				}
				for (int i = n - 1; i >= n - cnt; i--) {
					b[i][j] = 1;
				}
			}
			a = b;
		};

		for (int i = 1; i < (1 << (n * m)); i++) {
			for (int j = 0; j < n; j++) {
				for (int l = 0; l < m; l++) {
					int o = j * m + l;
					if (i >> o & 1) {
						a[j][l] = 1;
					} else {
						a[j][l] = 0;
					}
				}
			}
			map<vector<vector<int>>, int> mp;
			int res = 0;
			auto dfs = [&] (auto self, int step) -> void {
				if (res > k) {
					return ;
				}
				if (!mp[a]) {
					mp[a] = 1;
					res++;
				} else {
					return ;
				}
				if (step > 100) {
					return ;
				}
				vector b = a;
				do_U();
				self(self, step + 1);
				a = b;
				do_D();
				self(self, step + 1);
				a = b;
				do_L();
				self(self, step + 1);
				a = b;
				do_R();
				self(self, step + 1);
			};
			dfs(dfs, 0);
	
			if (res == k) {
				cout << "k = " << k << " is ok" << endl;
				for (int j = 0; j < n; j++) {
					for (int l = 0; l < m; l++) {
						int o = j * m + l;
						if (i >> o & 1) {
							cout << "1";
						} else {
							cout << "0";
						}
					}
					cout << "\n";
				}
				break;
			}
		}
	}
}


signed main() {
	fre(test);
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

当 \(n,m \ge 3\) 时，分出以下情况，打表找规律（听着难，实际上打出字典序最小的一个就能看出来）：

• \(k=1\)，把所有格子填满。
• \(k=2\)，把第一行填满。
• \(k=3\)，把第二行填满。
• \(k=4\)，填 \((1,1)\)。
• \(k=5\)，此时合法的局面需要满足移动一次后向任意方向移动都没意义。当 \(n=m\) 时填满任意一条对角线是好想的。\(n \neq m\) 时考虑把 \(n\times m\) 分成若干个 \(x\times x\) 的子矩阵，每个子矩阵填满一条对角线。此时可取 \(x = \gcd(n, m)\)。
• \(k=6\)， 填 \((1, 2)\)。
• \(k=7\)，填 \((2, 1)\land (1,x),x\in[2, m]\)。
• \(k=9\)，填 \((1, 2)\land (2, 1)\)。
• \(k=11\)，填 \((1, 3)\land (2, 1)\)。
• \(k=13\)，填 \((1, 3)\land (3, 1)\)。

代码写的比较 shit，如果把 \(n=2\) 和 \(m=2\) 单独列出来会直观很多，但我懒得改 shit 了。

时间复杂度 \(O(nm)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff
#define NO (void)(cout << "No\n")


//-------------- templates above --------------


void solve() {
	int n, m, k;
	cin >> n >> m >> k;
	if (k == 1) {
		cout << "Yes\n";
		for (int i = 0; i < n; i++, cout << "\n") {
			for (int j = 0; j < m; j++) {
				cout << '*';
			}
		}
		return ;
	}
	auto print = [&] (vector<array<int, 2>> a) -> void {
		cout << "Yes\n";
		for (int i = 0; i < n; i++, cout << "\n") {
			for (int j = 0; j < m; j++) {
				bool ok = false;
				for (auto [x, y] : a) {
					if (x == i + 1 && y == j + 1) {
						ok = true;
						break;
					}
				}
				cout << (ok ? '*' : '-');
			}
		}
	};
	auto printl = [&] (int x, int y) -> void {
		cout << "Yes\n";
		for (int i = 0; i < n; i++, cout << "\n") {
			for (int j = 0; j < m; j++) {
				if ((x && x == i + 1) || (y && y == j + 1)) {
					cout << "*";
				} else {
					cout << "-";
				}
			}
		}
	};

	if (n == 1 && m == 1) {
		NO;
	} else if (min(n, m) == 1 && max(n, m) == 2) {
		k == 2 ? print({{1, 1}}) : NO;
	} else if (min(n, m) == 1) {
		if (k == 2) {
			print({{1, 1}});
		} else if (k == 3) {
			n == 1 ? print({{1, 2}}) : print({{2, 1}});
		} else {
			NO;
		}
	} else if (k == 4) {
		print({{1, 1}});
	} else if (n == 2 && m == 2) {
		if (k == 2) {
			print({{1, 1}, {1, 2}});
		} else if (k == 5) {
			print({{1, 1}, {2, 2}});
		} else {
			NO;
		}
	} else if (n == 2 && m == 3) {
		if (k == 2) {
			printl(0, 1);
		} else if (k == 3) {
			printl(0, 2);
		} else if (k == 6) {
			print({{1, 2}});
		} else if (k == 7) {
			print({{1, 2}, {2, 1}});
		} else if (k == 9) {
			print({{1, 3}, {2, 1}});
		} else {
			NO;
		}
	} else if (n == 3 && m == 2) {
		if (k == 2) {
			printl(1, 0);
		} else if (k == 3) {
			printl(2, 0);
		} else if (k == 6) {
			print({{2, 1}});
		} else if (k == 7) {
			print({{1, 2}, {2, 1}});
		} else if (k == 9) {
			print({{1, 2}, {3, 1}});
		} else {
			NO;
		}
	} else {
		if (k == 2) {
			printl(1, 0);
		} else if (k == 3) {
			n > m ? printl(2, 0) : printl(0, 2);
		} else if (k == 5) {
			if (__gcd(n, m) == 1) {
				NO;
			} else {
				cout << "Yes\n";
				int g = __gcd(n, m);
				for (int i = 0; i < n; i++, cout << "\n") {
					for (int j = 0; j < m; j++) {
						int x = i % g;
						int y = j % g;
						if (x == y) {
							cout << "*";
						} else {
							cout << "-";
						}
					}
				}
			}
		} else if (k == 6) {
			n < m ? print({{1, 2}}) : print({{2, 1}});
		} else if (k == 7) {
			cout << "Yes\n";
			for (int i = 0; i < n; i++, cout << "\n") {
				for (int j = 0; j < m; j++) {
					if ((i == 1 && j == 0) || (i == 0 && j > 0)) {
						cout << "*";
					} else {
						cout << "-";
					}
				}
			}
		} else if (k == 9) {
			if (n == 2) {
				print({{1, 3}, {2, 1}});
			} else if (m == 2) {
				print({{3, 1}, {1, 2}});
			} else {
				print({{1, 2}, {2, 1}});
			}
		} else if (k == 11) {
			if (n == 2) {
				print({{1, 2}, {2, 1}, {1, 4}});
			} else if (m == 2) {
				print({{1, 2}, {2, 1}, {4, 1}});
			} else {
				print({{1, 3}, {2, 1}});
			}
		} else if (k == 13) {
			if (n == 2 || m == 2) {
				NO;
			} else {
				print({{1, 3}, {3, 1}});
			}
		} else {
			NO;
		}
	}
}


signed main() {

	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

---

B. 军训 II

感性地，排序后不整齐度最小。

\(ans1\) 可以单 \(\log\) 求，但允许 \(O(n^2)\) 就没必要自讨苦吃。

接着设每个连续段长 \(cnt_i\)，那么 \(ans2=2\prod cnt_i\)。系数来自升序排序和降序排序两种。

特判：所有数都相同时，升序和降序看作一种，\(ans2=\prod cnt_i\)。

时间复杂度 \(O(n^2)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define double long double
#define inf 0x3fffffffffffffff

constexpr int modp = 998244353;

void solve() {
	int n;
	cin >> n;
	vector<int> fac(n + 1);
	fac[0] = 1;
	for (int i = 1; i <= n; i++) {
		fac[i] = fac[i - 1] * i % modp;
	} 
	vector<int> a(n);
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	sort(a.begin(), a.end());
	int ans1 = 0;
	for (int i = 0; i < n; i++) {
		int mx = a[i], mn = a[i];
		for (int j = i; j < n; j++) {
			mx = max(mx, a[j]);
			mn = min(mn, a[j]);
			ans1 += mx - mn;
		}
	}

	int cnt = 1, ans2 = 1;
	for (int i = 1; i < n; i++) {
		if (a[i] != a[i - 1]) {
			ans2 *= fac[cnt];
			ans2 %= modp;
			cnt = 1;
		} else {
			cnt++;
		}
	}
	ans2 *= fac[cnt];
	ans2 %= modp;
	
	vector b = a;
	reverse(b.begin(), b.end());
	if (a != b) {
		ans2 *= 2;
		ans2 %= modp;
	}
	cout << ans1 << " " << ans2 << "\n";
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

---

C. 种树

将已经种了树的点称为黑点，否则白点。

两种错误的贪心举例：

• 两个黑点间夹 \(k\) 个白点，\(k\) 为偶数时用 \(\dfrac{k}{2}\) 次操作填满。
• 以两个或以上相连的黑点为界，每个连通块贡献为 \(\left\lceil \dfrac{白点个数}{2}\right\rceil\)。

反例对应如下。

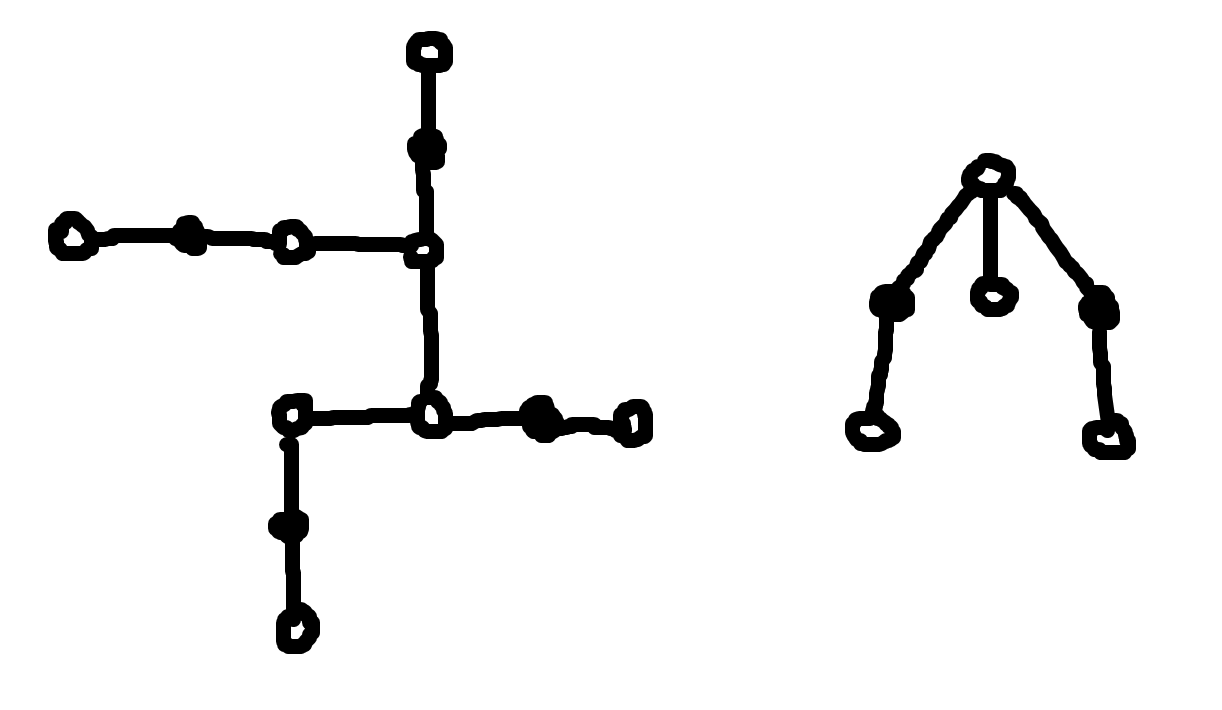
正确的贪心：任选一黑点为根 dfs，自下而上贪心，每次填两个。对于一个黑点：

• 若当前子树中白点数为偶数，填满。
• 否则考虑是否能把多余的一个涂色操作摊给当前黑点的父亲。

时间复杂度 \(O(n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff




//-------------- templates above --------------



void solve() {
	int n, m;
	cin >> n >> m;
	vector<int> a(n + 1);
	int rt = -1;
	for (int i = 1; i <= m; i++) {
		int x;
		cin >> x;
		a[x] = true;
		rt = x;
	}
	vector<vector<int>> adj(n + 1);
	for (int i = 1; i < n; i++) {
		int x, y;
		cin >> x >> y;
		adj[x].push_back(y);
		adj[y].push_back(x);
	}
	int ans = 0;
	vector<int> sz(n + 1);
	auto dfs = [&] (auto self, int x, int fath) -> void {
		sz[x] = a[x] == 0;
		for (auto y : adj[x]) {
			if (y == fath) {
				continue;
			}
			self(self, y, x);
			sz[x] += sz[y];
		}
		if (a[x]) {
			ans += sz[x] / 2;
			if (sz[x] % 2) {
				ans++;
				if (fath && a[fath] == 0) {
					a[fath] = 1;
					sz[fath]--;
				}
			}
			sz[x] = 0;
		}
	};
	dfs(dfs, rt, 0);
	cout << ans << "\n";
}


signed main() {

	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

---

G. 疯狂星期六

yyq 需要尽可能花多的钱，而他花的最多的钱数是可以处理出来的，即 \(X=\min(\sum \text{能摊到 yyq 上的菜钱}+T_1,a_1)\)。

令 \(mx_i\) 为第 \(i\) 个人能花在菜上的最多钱数，首先 \(mx_1=X-T_1\)，那么 \(mx_i=\min(a_i,mx_1-1)\)。

接着只需 check 是否存在一种满足上述条件的方案。

转化为网络流问题：

• 源点向每个菜连容量为菜钱的边。
• 每个菜向付它钱的两个人连容量为菜钱的边。
• 每个人向汇点连容量为 \(mx_i\) 的边。

check 成功当且仅当最大流 \(=\) 总菜钱。

时间复杂度 \(O(n\sqrt{m})\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff

struct Dinic {
	struct Edge {
		int x, cap;
		Edge(int x, int cap) : x(x), cap(cap) {} 
	};
	int n;
	vector<Edge> e;
	vector<vector<int>> adj;
	vector<int> dep, cur;
	Dinic(int size) {
		this->n = size;
		adj.resize(n + 1);
	}
	void add(int x, int y, int cap) {
		adj[x].push_back(e.size());
		e.push_back({y, cap});
		adj[y].push_back(e.size());
		e.push_back({x, 0});
	}
	int bfs(int S, int T) {
		dep.assign(n + 1, -1);
		queue<int> q;
		q.push(S);
		dep[S] = 0;
		while (!q.empty()) {
			int x = q.front();
			q.pop();
			for (auto i : adj[x]) {
				auto [y, cap] = e[i];
				if (cap > 0 && dep[y] == -1) {
					dep[y] = dep[x] + 1;
					if (y == T) {
						return true;
					}
					q.push(y);
				}
			}
		}
		return false;
	}
	int dfs(int x, int T, int limit) {
		if (x == T) {
			return limit;
		}
		int r = limit;
		for (int &i = cur[x]; i < adj[x].size(); i++) {
			const int j = adj[x][i];
			auto [y, cap] = e[j];
			if (cap > 0 && dep[y] == dep[x] + 1) {
				int t = dfs(y, T, min(r, cap));
				e[j].cap -= t;
				e[j ^ 1].cap += t;
				r -= t;
				if (r == 0) {
					return limit;
				}
			}
		}
		return limit - r;
	}
	int dinic(int S, int T) {
		int flow = 0;
		while (bfs(S, T)) {
			cur.assign(n + 1, 0);
			flow += dfs(S, T, inf); 
		} 
		return flow;
	}
};



//-------------- templates above --------------



void solve() {
	int n, m;
	cin >> n >> m;
	vector<int> a(n + 1), Taxi(n + 1);
	for (int i = 1; i <= n; i++) {
		cin >> a[i] >> Taxi[i];
	}
	vector<array<int, 3>> dish(m + 1);
	vector<int> mxcost(n + 1);
	int all = 0;
	for (int i = 1; i <= m; i++) {
		int x, y, w;
		cin >> x >> y >> w;
		dish[i] = {x, y, w};
		all += w;
		if (x == 1 || y == 1) {
			mxcost[1] += w;
		}
	}
	mxcost[1] = min(a[1], mxcost[1] + Taxi[1]);
	for (int i = 2; i <= n; i++) {
		mxcost[i] = min(a[i], mxcost[1] - 1) - Taxi[i];
		if (mxcost[i] < 0) {
			cout << "NO\n";
			return ;
		}
	}
	mxcost[1] -= Taxi[1];

	int S = m + n + 1;
	int T = m + n + 2;
	Dinic G(T);
	for (int i = 1; i <= m; i++) {
		auto [x, y, w] = dish[i];
		G.add(S, i, w);
		G.add(i, m + x, w);
		G.add(i, m + y, w);
	} 
	for (int i = 1; i <= n; i++) {
		G.add(m + i, T, mxcost[i]);
	}
	if (G.dinic(S, T) == all) {
		cout << "YES\n";
	} else {
		cout << "NO\n";
	}
}


signed main() {

	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

---

J. 找最小

令 \(c_i=a_i\oplus b_i\)，\(A=\oplus_{i=1}^{n} a_i\)，\(B=\oplus_{i=1}^{n} b_i\)。

根据异或运算的自反性，题目转化为需要选一些 \(c_i\)（设选出的 \(c_i\) 的异或和为 \(C\)）使得 \(\max(A\oplus C,B\oplus C)\) 最小。

联想到线性基，其能解决这样一类问题：从一堆数中选出若干个数，它们的异或和最大/最小。

插入操作不用修改，查询时不妨将 \(\max(A,B)\) 作为初值，代表已经选出这么多。

随后从高位向低位贪心，判断到某位异或之后 \(\max\) 变小就更新即可。

时间复杂度 \(O(n\log w)\)，\(w\) 为值域。

Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define double long double
#define inf 0x3fffffffffffffff

struct Node {
	int n;
	vector<int> p;
	Node(int _n) : n(_n), p(_n + 1) {}
	void insert(int x) {
		for (int i = n; i >= 0; i--) {
			if (!(x >> i)) {
				continue;
			}
			if (!p[i]) {
				p[i] = x;
				break;
			}
			x ^= p[i];
		}
	}
	int getans(int st1, int st2) {
		int res = max(st1, st2);
		int X = st1, Y = st2;
		for (int i = n; i >= 0; i--) {
			if (max(X ^ p[i], Y ^ p[i]) < res) {
				X ^= p[i];
				Y ^= p[i];
				res = max(X, Y);
			}
		}
		return res;
	}
};

void solve() {
	int n;
	cin >> n;
	vector<int> a(n + 1), b(n + 1);
	int val1 = 0, val2 = 0;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		val1 ^= a[i];
	}
	for (int i = 1; i <= n; i++) {
		cin >> b[i];
		val2 ^= b[i];
	}
	Node t(31);
	for (int i = 1; i <= n; i++) {
		t.insert(a[i] ^ b[i]);
	}
	cout << t.getans(val1, val2) << "\n";
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

---

K. 取沙子游戏

当 \(n\) 为奇数时，先手拿 \(1\)，之后后手和先手都只能轮流拿 \(1\)，先手必胜。

否则，先手只能拿偶数，一种策略是每次拿 $ $，之后后手无论拿什么，先手跟着拿就行。

故当 \(\text{lowbit(n)}\le k\) 时，先手必胜。否则无论拿 \(1\sim k\) 中的多少，\(\text{lowbit(n)}\) 都会落到 \(k\) 以内，让后手取得胜利。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff




//-------------- templates above --------------



void solve() {
	int n, k;
	cin >> n >> k;
	if ((n & -n) <= k) {
		cout << "Alice\n";
	} else {
		cout << "Bob\n";
	}
}


signed main() {

	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}