【题解】AtCoder Beginner Contest 222 D~G

D. Between Two Arrays

Problem

好题

题意：给定长为 \(n\) 的单调不下降的整数序列 \(a,b\)，且满足 \(a_i\le b_i\)。求满足 \(a_i\le c_i\le b_i\) 的单调不下降的整数序列 \(c\) 的数量。

\(1\le n\le 3000\)，\(0\le a_i\le b_i\le 3000\)。

前缀和优化 dp 经典题。

令 \(dp_{i,j}\) 表示长度为 \(i\) 且以 \(j\) 结尾的单调不下降序列数量。则： \[dp_{i,j}=\sum\limits_{k\in [0,j] \text{ }\cap \text{ }[a_{i-1},b_{i-1}]} dp_{i-1,k}\] 那么我们需要枚举 \(i,j,k\)，时间复杂度 \(O(n\alpha^2)\)，\(\alpha\) 为值域。

利用前缀和优化，令 \(s_{i,j}=\sum\limits_{j\in[0,j]}dp_{i,j}\)，\(O(\alpha)\) 便能完成转移。

总时间复杂度 \(O(n\alpha)\) 。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;

template<const int T>
struct ModInt {
    const static int mod = T;
    int x;
    ModInt(int x = 0) : x(x % mod) {}
    int val() { return x; }
    ModInt operator + (const ModInt &a) const { int x0 = x + a.x; return ModInt(x0 < mod ? x0 : x0 - mod); }
    ModInt operator - (const ModInt &a) const { int x0 = x - a.x; return ModInt(x0 < 0 ? x0 + mod : x0); }
    ModInt operator * (const ModInt &a) const { return ModInt(1LL * x * a.x % mod); }
    ModInt operator / (const ModInt &a) const { return *this * a.inv(); }
    bool operator == (const ModInt &a) const { return x == a.x; };
    bool operator != (const ModInt &a) const { return x != a.x; };
    void operator += (const ModInt &a) { x += a.x; if (x >= mod) x -= mod; }
    void operator -= (const ModInt &a) { x -= a.x; if (x < 0) x += mod; }
    void operator *= (const ModInt &a) { x = 1LL * x * a.x % mod; }
    void operator /= (const ModInt &a) { *this = *this / a; }
    friend ModInt operator + (int y, const ModInt &a){ int x0 = y + a.x; return ModInt(x0 < mod ? x0 : x0 - mod); }
    friend ModInt operator - (int y, const ModInt &a){ int x0 = y - a.x; return ModInt(x0 < 0 ? x0 + mod : x0); }
    friend ModInt operator * (int y, const ModInt &a){ return ModInt(1LL * y * a.x % mod);}
    friend ModInt operator / (int y, const ModInt &a){ return ModInt(y) / a;}
    friend ostream &operator<<(ostream &os, const ModInt &a) { return os << a.x;}
    friend istream &operator>>(istream &is, ModInt &t){return is >> t.x;}

    ModInt pow(int64_t n) const {
        ModInt res(1), mul(x);
        while(n){
            if (n & 1) res *= mul;
            mul *= mul;
            n >>= 1;
        }
        return res;
    }
    
    ModInt inv() const {
        int a = x, b = mod, u = 1, v = 0;
        while (b) {
            int t = a / b;
            a -= t * b; swap(a, b);
            u -= t * v; swap(u, v);
        }
        if (u < 0) u += mod;
        return u;
    }
    
};
using mint = ModInt<modp>;

void solve()
{
	int n=read();
	vector<int> a(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	vector<int> b(n+1);
	for(int i=1;i<=n;++i) {
		b[i]=read();
	}
	vector<vector<mint>> dp(n+1,vector<mint>(3002,0));
	vector<vector<mint>> sum(n+1,vector<mint>(3002,0));
	dp[0][0]=1;
	for(int i=1;i<=3000;++i) {
		sum[0][i]=1;
	}
	for(int i=1;i<=n;++i) {
		for(int j=a[i];j<=b[i];++j) {
			int l=a[i-1],r=min(j,b[i-1]);
			dp[i][j]+=sum[i-1][r+1]-sum[i-1][l];
		}
		sum[i][1]=dp[i][0];
		for(int j=1;j<=3000;++j) {
			sum[i][j+1]=sum[i][j]+dp[i][j];
		}
	}
	mint res=0;
	for(int i=0;i<=3000;++i) {
		res+=dp[n][i];
	}
	printf("%lld\n",res);
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

E. Red and Blue Tree

Problem

好题

题意：给定一棵 \(n\) 个点的树和一个长为 \(m\) 的序列 \(a\) 和一个整数 \(K\)，你需要给这颗树上的边染蓝色或染红色。合法的染色方案满足从 \(a_1\) 开始依次途径 \(a_2,a_3,\dots ,a_{n-1}\) 最后到达 \(a_n\) 的路径中经过的蓝边数总和 \(B\) 和红边数总和 \(R\) ，有 \(R-B=K\)。求方案数。

\(2\le n\le 1000\)，\(2\le m\le 100\)。

对每两个相邻的数都跑 \(\text{dfs}\) 记录每条边 $i $ 的经过次数 \(C_i\)。

问题转化为：将 \(C_1,C_2,...,C_{n-1}\) 分成两个集合使得两个集合里元素的和 \(R\) 和 \(B\) 满足 \(R-B=K\)。

令 \(C_1+C_2+...+C_{n-1}=S\) , 则

\[\begin{cases}S=R+B\\R-B=K \end{cases}\rightarrow 2R=S+K\rightarrow R=\frac{S+K}{2}\]

问题转化为从 \(C_1,C_2,...,C_{n-1}\) 中选择若干个数使得和为 \(\frac{S+K}{2}\)，dp 即可 。

具体的，令 \(dp_x\) 表示使得和为 \(x\) 的方案数， \(dp_x=\sum dp_{x-C_i}\) 。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read(),m=read(),K=read();
	vector<int> a(m+1);
	for(int i=1;i<=m;++i) {
		a[i]=read();
	}
	vector<vector<array<int,2>>> adj(n+1);
	for(int i=1;i<n;++i) {
		int x=read(),y=read();
		adj[x].push_back({y,i});
		adj[y].push_back({x,i});
	}
	vector<int> cnt(n);
	auto dfs = [&] (auto self,int x,int fath,int goal) {
		if(x==goal) {
			return true;
		}
		for(auto [y,i]:adj[x]) {
			if(y!=fath) {
				if(self(self,y,x,goal)) {
					cnt[i]++;
					return true;
				}
			}
		}
		return false;
	};
	for(int i=1;i<m;++i) {
		dfs(dfs,a[i],0,a[i+1]);
	}

	int S=0;
	for(int i=1;i<n;++i) {
		S+=cnt[i];
	}
	if((S+K)%2 || S+K<0) {
		puts("0");
		return ;
	}

	vector<int> dp(1e5+10);
	dp[0]=1;
	for(int i=1;i<n;++i) {
		for(int x=1e5;x>=cnt[i];--x) {
			dp[x]+=dp[x-cnt[i]];
			dp[x]%=modp;
		}
	}
	printf("%lld\n",dp[(S+K)/2]);
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

F. Expensive Expense

problem

好题

题意：树上每个点有权值 \(a_i\)，边也有边权 \(w_i\)。令 \(dis_{i,j}\) 表示 \(i\) 到 \(j\) 的简单路径长度 , 对于每一个 \(i\) 求 \(\sum\limits_{j=1,j\neq i}^n max(dis_{i,j}+a_j)\)。

\(2\le n\le 2\times 10^5\)，\(1\le c_i,w_i \le 10^9\)。

方法一：（树的直径的性质）

一个结论：距离树上任意一点最远的点一定是直径两个端点中的一个。（这也是两次 \(\text{dfs}\) 能够求树的直径的依据）

但这里有点权，那我们可以变通。

两次 \(\text{dfs}\) 求树的直径时，将比较 \(dis_i\) 换成比较 \(dis_i+a_i\)。这样求出来的 “直径” 就是整颗树 \(dis_i+ a_i\) 最大的路径。

确定了直径的两个端点 \(ml,mr\) 后，再次应用 \(\text{dfs}\) 求出两个端点到所有点的简单路径距离 \(disl\) 和 \(disr\)。

那么对于每个 \(i\)，\(ans=\max(disl_{i}+a_{ml},disr_{i}+a_{mr})\)。

Code 1

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read();
	vector<vector<array<int,2>>> adj(n+1);
	for(int i=1;i<=n-1;++i) {
		int x=read(),y=read(),w=read();
		adj[x].push_back({y,w});
		adj[y].push_back({x,w});
	}
	vector<int> a(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	auto dfs = [&](auto self,int x,int fath,vector<int> &dis) -> void {
		for(auto [y,z]:adj[x]) {
			if(y!=fath) {
				dis[y]=dis[x]+z;
				self(self,y,x,dis);
			}
		}
	};
	vector<int> dis(n+1),dis1(n+1),dis2(n+1);
	dfs(dfs,1,0,dis);
	int ml=-1;
	for(int i=1,maxn=0;i<=n;++i) {
		if(dis[i]+a[i]>maxn) {
			maxn=dis[i]+a[i];
			ml=i;
		}
	}
	dfs(dfs,ml,0,dis1);
	int mr=-1;
	for(int i=1,maxn=0;i<=n;++i) {
		if(i!=ml && dis1[i]+a[i]>maxn) {
			maxn=dis1[i]+a[i];
			mr=i;
		}
	}
	dfs(dfs,mr,0,dis2);
	for(int i=1;i<=n;++i) {
		int res=0;
		if(i!=ml) {
			res=max(res,dis1[i]+a[ml]);
		}
		if(i!=mr) {
			res=max(res,dis2[i]+a[mr]);
		} 
		printf("%lld\n",res);
	}
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

方法二：（换根dp）

第一次 \(\text{dfs}\)，\(dp_{i,0/1}\) 代表 \(i\) 的子树内答案的最大值/次大值。那么有： \[dp_{x}=\max_{y\in son[x]}(dp_{x},dp_{y}+w,a_y+w)\] 第二次 \(\text{dfs}\) ，可以画图分析：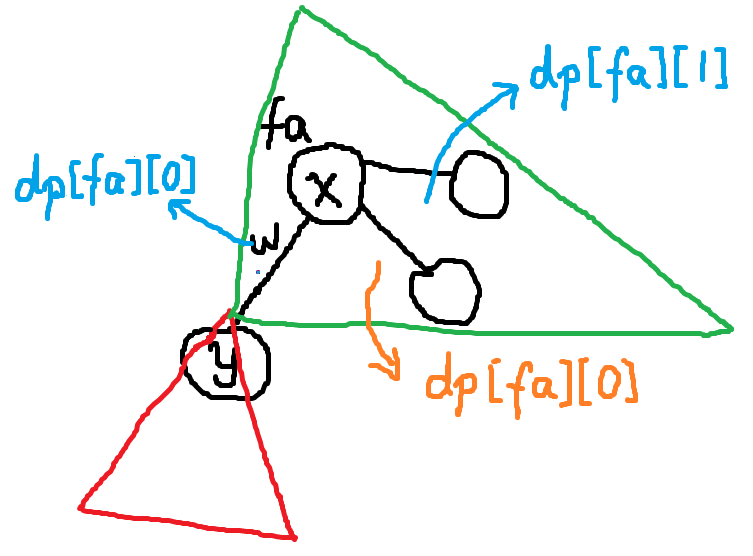

向下 \(\text{dfs}\) 时子树内的贡献没有改变，我们只需要分析另一边（绿色部分）多出了哪些贡献。

假设我们刚刚走过了边 \(fa\to y\)，分为两种情况：

1. （橙字）\(dp_{fa,0}\) 从非 \(y\) 子树内转移而来，那么： \[dp_y=\max(dp_y,dp_{fa,0}+w)\]

2. （蓝字）\(dp_{fa,0}\) 从 \(y\) 的子树内转移而来，非子树部分的最大值实际就是 \(fa\) 节点对应的次大值，那么： \[dp_y=\max(dp_y,dp_{fa,1}+w)\]

最后更新答案。

Code 2

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read();
	vector<vector<array<int,2>>> adj(n+1);
	for(int i=1;i<n;++i) {
		int x=read(),y=read(),w=read();
		adj[x].push_back({y,w});
		adj[y].push_back({x,w});
	}
	vector<int> a(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	vector<vector<int>> dp(n+1,vector<int>(2,0));
	vector<int> from(n+1);
	auto dfs = [&] (auto self,int x,int fa) -> void {
		for(auto [y,w]:adj[x]) {
			if(y!=fa) {
				self(self,y,x);
				int t=max(a[y],dp[y][0])+w;
				if(t>dp[x][0]) {
					dp[x][1]=dp[x][0];
					dp[x][0]=t;
					from[x]=y;
				} else if(t>dp[x][1]) {
					dp[x][1]=t;
				}
			}
		}
	};
	dfs(dfs,1,0);
	auto dfs2 = [&] (auto self,int x,int fa,int w) -> void {
		int t=a[fa]+w;
		if(from[fa]!=x) {
			t=max(t,dp[fa][0]+w);
		} else {
			t=max(t,dp[fa][1]+w);
		}
		if(t>dp[x][0]) {
			dp[x][1]=dp[x][0];
			dp[x][0]=t;
			from[x]=fa;
		} else if(t>dp[x][1]) {
			dp[x][1]=t;
		}
		for(auto [y,w]:adj[x]) {
			if(y!=fa) {
				self(self,y,x,w);
			}
		}
	};
	for(auto [y,w]:adj[1]) {
		dfs2(dfs2,y,1,w);
	}
	for(int i=1;i<=n;++i) {
		printf("%lld\n",dp[i][0]);
	}
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

G. 222

Problem

好题

题意：幸运数字是由若干个 \(2\) 构成的数字（如 \(2,22,222,\dots\) ）。给定正整数 \(k\)，当 \(k\) 的倍数第一次属于某个幸运数字时。输出该倍数由多少个 \(2\) 组成。若不存在 \(k\) 的倍数是幸运数字，输出 \(-1\)。

幸运数字可以表示为 \(2\times \dfrac{10^x-1}{9}\)。

问题转化为寻求最小的 \(x\) 使得： \[\begin{align}2\times \dfrac{10^x-1}{9}&\equiv 0 \pmod{k} \\2\times(10^x-1) &\equiv 0 \pmod{9k} \\10^x-1 &\equiv 0 \pmod{\dfrac{9k}{\gcd(k,2)}} \\10^x &\equiv 1 \pmod{\dfrac{9k}{\gcd(k,2)}}\end{align}\] 转化为了 \(a^x\equiv b \pmod{P}\) 的形式，运用 BSGS 算法即可求解。

还可以运用欧拉函数。

回忆欧拉定理：对于互质的正整数 \(a,n\) 有 \(a^{\varphi(n)}\equiv1\pmod{n}\) .

我们令 \(p=\dfrac{9k}{\gcd(k,2)} ,x=\varphi(p)\)，则 \(10^{\varphi(p)}\equiv1\pmod{p}\)，可以直接得到一个可行解。

虽然 \(\varphi(p)\) 不一定是满足条件的正整数，但答案一定是其因子，枚举即可。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;

//欧拉函数
int eular(int n)
{
    int ret=1;
    for(int i=2;i<=n/i;++i) {
    	if(n%i==0) {
        	n/=i;
        	ret*=i-1;
        }
        while(n%i==0) {
        	n/=i;
        	ret*=i;
        }
    }
    if(n>1) {
    	ret*=n-1;
    }
    return ret;
}

inline int qpow(int k,int n,int p) {
	int s=1;
	for(;n;n>>=1,k=k*k%p) if(n&1) s=s*k%p;
	return s;
}
 
void solve()
{
	int K=read();
	int p=9*K/__gcd(K,2ll);
	int n=eular(p);
	if(__gcd(10ll,p)>1) {
		puts("-1");
		return ;
	}
	int ans=n;
	for(int i=1;i<=sqrtl(n);++i) {
		if(n%i==0) {
			if(qpow(10,i,p) == 1) {
				ans=min(ans,i);
			}
			if(qpow(10,n/i,p) == 1) {
				ans=min(ans,n/i);
			}
		}
	}
	printf("%lld\n",ans);
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}