【题解】Codeforces Round 902 (Div. 2, based on COMPFEST 15 - Final Round) 5 of 7

A. Goals of Victory

Problem

赢的场次一定和输的场次相等。

即 \(\sum\limits_{i=1}^{n} a_i = 0\)。故 \(ans=-\sum\limits_{i=1}^{n-1}a_i\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read();
	vector<int> a(n);
	int sum=0;
	for(int i=1;i<n;++i) {
		a[i]=read();
		sum+=a[i];
	}
	printf("%lld\n",-1*sum);
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

B. Helmets in Night Light

Problem

题意：须弥除了草神外有 \(n\) 个居民。草神要通过虚空终端向所有 \(n\) 个人传递公告，其直接向一个居民传递的代价为 \(p\)。居民 \(i\) 一旦得知，也可以向其它人传递，但最多直接传递给 \(a_i\) 个人且每个人的传递代价为 \(b_i\)。求最小代价。

\(1\le n,a_i,b_i \le 10^5\)。

考虑贪心。因为对于向单个人的传递代价，肯定是越小越好。

一开始，草神必然至少通知一个人，代价为 \(p\)。

之后将代价 \(b_i\) 排序后从小到大选择，若 \(b_i>p\)，肯定不优，考虑把剩余的通知任务全堆给草神。

否则累加 \(a_i\)，当选择的 \(a_i\) 之和超过 \(n-1\) 时就代表通知了所有人。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read(),p=read();
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	for(int i=1;i<=n;++i) {
		b[i]=read();
	}
	vector<int> order(n);
	iota(order.begin(),order.end(),1);
	sort(order.begin(),order.end(),[&](int i,int j){
		return b[i]<b[j];
	});
	int res=0,sum=0;
	bool fir=true;
	for(auto i:order) {
		if(b[i]<=p) {
			if(fir) {
				fir=false;
				res+=p;
				sum++;
			}
			int add=min(n-sum,a[i]);
			sum+=add;
			res+=b[i]*add;
			if(sum==n) {
				break;
			}
		} else {
			res+=(n-sum)*p;
			break;
		}
	}
	printf("%lld\n",res);
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

C. Joyboard

Problem

题意：给定长为 \(n+1\) 的序列 \(a\)，一开始全为空。你可以给 \(a_{n+1}\) 填上 \(0\sim m\) 中的一个，之后从右向左构造 \(a_i=a_{i+1} \pmod {i}\)。求最终序列有 \(k\) 个不同的数的方案数。

\(1\le n\le 10^9\)，\(0\le m \le 10^9\)，\(1\le k \le n+1\)。

随便列举一下就图穷匕见了。

当 \(n=6\) 时有：

\[\begin{alignat}{7}a_1 &\quad& a_2 &\quad& a_3 &\quad& a_4 &\quad& a_5 &\quad& a_6 &\quad& a_7\\0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 \\0 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 \\0 &\quad& 0 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 2 \\0 &\quad& 0 &\quad& 0 &\quad& 3 &\quad& 3 &\quad& 3 &\quad& 3 \\ &\quad& &\quad& &\quad& \vdots &\quad& &\quad& &\quad& \\0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 6 \\0 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 7 \\0 &\quad& 0 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 8 \\0 &\quad& 0 &\quad& 0 &\quad& 3 &\quad& 3 &\quad& 3 &\quad& 9 \\ &\quad& &\quad& &\quad& \vdots &\quad& &\quad& &\quad& \\0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 0 &\quad& 12 \\0 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 1 &\quad& 13 \\0 &\quad& 0 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 2 &\quad& 14 \\ &\quad& &\quad& &\quad& \vdots &\quad& &\quad& &\quad& \\\end{alignat}\]

生成的序列一定最多经过两次衰减变为 \(0\)。

那么当 \(k>3\) 时一定无解。

令 \(a_{n+1}=x\) ：

当 \(k=1\) 时，显然只有 \(x=0\) 符合题意。

当 \(k=2\) 时，首先对于 \(n\mid x\) 一定符合题意，其次 \(x\in[1,n-1]\) 只衰减一次，同样符合题意。

当 \(k=3\) 时，容斥一下就好了。

\[ans=\begin{cases}1 &,k=1 \\m &,k=2,m\le n \\n+\lfloor \frac{m-n}{n}\rfloor &,k=2,m > n \\m-n-\lfloor \frac{m-n}{n}\rfloor &,k=3,m > n \\0 &,others\end{cases}\]

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read(),m=read(),k=read();
	if(k==1) {
		puts("1");
		return ;
	} 
	if(k>3) {
		puts("0");
		return ;
	}
	int div=k/n,cnt=0;
	if(m<=n) {
		cnt=m;
	} else {
		cnt=m/n;
		cnt+=(n-1);
	}
	if(k==2) {
		printf("%lld\n",cnt);
	} else {
		printf("%lld\n",m-cnt);
	}
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

D. Effects of Anti Pimples

Problem

好题

题意：给定长度为 \(n\) 的数列，一开始全为白色。你可以任意选一些索引，将对应位置涂黑。然后对于每一个涂黑的位置，将它索引的所有倍数的位置涂绿（不可覆盖黑）。定义该状态的价值为黑色和绿色所有位置上数的最大值。涂黑方案有 \(2^n-1\) 种，求所有方案价值总和。

\(1\le n \le 10^5\)，\(0\le a_i \le 10^5\)。

令 \(f_i\) 表示位置 \(i\) 的价值。

因为将 \(a_i\) 涂成黑色的同时所有 \(i\mid j\) 的 \(a_j\) 被涂成了绿色。

而这段子序列的价值只和最大值有关，故 \(f_i=\max\limits_{i\mid j} a_j\)。

考虑 \(f_i\) 对答案的贡献。

一个结论，\(n\) 个数的所有子集中包含某个下标的子集有 \(2^{n-1}\) 个。

为什么？

\(n\) 个数共有 \(2^n-1\) 个子集，去掉某个下标后剩下 \(n-1\) 个数共有 \(2^{n-1}-1\) 个子集。

这 \(2^{n-1}-1\) 个子集都不包含那个下标。故包含那个下标的子集有 \(2^n-1-(2^{n-1}-1)=2^{n-1}\) 个。

故最大的 \(f_i\) 对答案的贡献是 \(f_i\times 2^{n-1}\)。

而次大 \(f_i\) 对答案的贡献是 \(f_i\times 2^{n-2}\)。因为次大值若有贡献必不能包含最大值，相当于除去最大 \(f_i\) 剩下 \(n-1\) 个数，被 \(2^{n-2}\) 个集合包含。

以此类推。

故答案为 \(\sum\limits_{i=1}^{n} 2^{i-1} f_i\) 。其中 \(f_i\) 从小到大排序。

时间复杂度 \(O(n\ln n)\) 。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;

template<const int T>
struct ModInt {
    const static int mod = T;
    int x;
    ModInt(int x = 0) : x(x % mod) {}
    int val() { return x; }
    ModInt operator + (const ModInt &a) const { int x0 = x + a.x; return ModInt(x0 < mod ? x0 : x0 - mod); }
    ModInt operator - (const ModInt &a) const { int x0 = x - a.x; return ModInt(x0 < 0 ? x0 + mod : x0); }
    ModInt operator * (const ModInt &a) const { return ModInt(1LL * x * a.x % mod); }
    ModInt operator / (const ModInt &a) const { return *this * a.inv(); }
    bool operator == (const ModInt &a) const { return x == a.x; };
    bool operator != (const ModInt &a) const { return x != a.x; };
    void operator += (const ModInt &a) { x += a.x; if (x >= mod) x -= mod; }
    void operator -= (const ModInt &a) { x -= a.x; if (x < 0) x += mod; }
    void operator *= (const ModInt &a) { x = 1LL * x * a.x % mod; }
    void operator /= (const ModInt &a) { *this = *this / a; }
    friend ModInt operator + (int y, const ModInt &a){ int x0 = y + a.x; return ModInt(x0 < mod ? x0 : x0 - mod); }
    friend ModInt operator - (int y, const ModInt &a){ int x0 = y - a.x; return ModInt(x0 < 0 ? x0 + mod : x0); }
    friend ModInt operator * (int y, const ModInt &a){ return ModInt(1LL * y * a.x % mod);}
    friend ModInt operator / (int y, const ModInt &a){ return ModInt(y) / a;}
    friend ostream &operator<<(ostream &os, const ModInt &a) { return os << a.x;}
    friend istream &operator>>(istream &is, ModInt &t){return is >> t.x;}

    ModInt pow(int64_t n) const {
        ModInt res(1), mul(x);
        while(n){
            if (n & 1) res *= mul;
            mul *= mul;
            n >>= 1;
        }
        return res;
    }
    
    ModInt inv() const {
        int a = x, b = mod, u = 1, v = 0;
        while (b) {
            int t = a / b;
            a -= t * b; swap(a, b);
            u -= t * v; swap(u, v);
        }
        if (u < 0) u += mod;
        return u;
    }
    
};
using mint = ModInt<modp>;

void solve()
{
	int n=read();
	vector<int> a(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	for(int i=1;i<=n;++i) {
		for(int j=i;j<=n;j+=i) {
			a[i]=max(a[i],a[j]);
		}
	}
	sort(a.begin()+1,a.end());
	mint res=0,sum=0;
	for(int i=1;i<=n;++i) {
		sum == 0 ? sum=1 : sum=sum*2;
		res+=sum*a[i];
	}
	printf("%lld\n",res);
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

对于以下代码段，时间复杂度为 \(O(n\ln n)\) 。

for(int i=1;i<=n;++i) {
    for(int j=i;j<=n;j+=i) {
        //do something
    }
}

因为执行次数 \(\frac{n}{1}+\frac{n}{2}+\frac{n}{3}+\dots +\frac{n}{n} = n(1+\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n})\)。调和级数的和约为 \(\ln n\)。

E. Autosynthesis

Problem

好题

题意：给定长为 \(n\) 的正整数序列 \(a\)。你要将这个序列划分成两个不交的子序列，满足其中一个子序列的下标构成的集合等于另一个子序列的值构成的集合。输出作为值的那一个子序列。

\(1\le a_i\le n \le 2\times 10^5\)。

转换为图论模型，对每个 \(i\in[1,n]\) 连边 \(i\to a_i\)，会形成一颗基环内向树。

考虑一个经典模型——置换环。

那是什么

对于一个任意 \(1\sim n\) 的排列 \(a\) ，连边 \(i\to a_i\)，得到的图一定是由一个或多个环组成（一个点看作长度为 \(1\) 的环），称作置换环。

其意义在于，位于一个长度为 \(L\) 的置换环内的元素，经历最少 \(L-1\) 次元素交换便能使元素在原序列中有序。

于是对于任意一个排列，两两交换其中元素使其变得单调增的最小交换次数就是 \(n-\text{置换环个数}\) 。

如果序列 \(a\) 是排列，只需要满足 \(a\) 的所有置换环长度均为偶数。

因为可以间隔黑白染色，染成黑色和白色的点的集合正好对应题中的两个序列。

例如，有排列 4 3 6 5 7 8 1 2 ，连边后如下图。

2

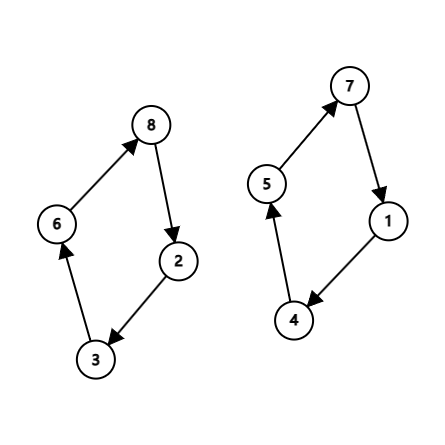
下标集合 1,2,5,6 或 1,3,5,8 或 3,4,7,8 等均符合题意。

为什么间隔染色正确？因为对于一条有向边，总是一个索引指向对应的值。

而挑选出的 \(\frac{n}{2}\) 个点的出边指向的 “值的点集” 正好与 “索引点集” 互补！

那么剩下的 \(\frac{n}{2}\) 的 “值的点集” 就必然与 “索引点集” 相同。

好，但现在 \(a\) 并不是排列，但这也说明有一些数不会在 \(a\) 中出现：

• 若点 \(i\) 被选入索引点集，则存在一个没被选的点 \(j\) 满足 \(a_j=i\)。
• 若对点 \(i\) 有 \(\exists\mkern-10mu/ \text{ }j\) 使得 \(a_j=i\)，那这个点一定属于值的点集。

这意味这 \(n\) 个数中有一些数的状态是确定的。

手玩一下样例，模拟一下将索引点集对应的值逐步删掉，只留下值的集合的过程：

Input：
5
3 4 2 2 3
Output：
3
3 2 3

首先 \(1\) 没在 \(a\) 中出现，\(1\) 不可能属于索引点集，那么 \(a[1]\) 永远不能被删掉。

同理 \(a[5]\) 也永远不能被删掉。

为保证 \(a[1]=3\) 不被删，那么 \(a[3]\) 必然被删掉。

为保证 \(a[3]=2\) 必然被删，所以 \(a[2]\) 永远不能被删掉？不，不一定。

因为场上不只有一个 \(2\)，\(a[4]\) 也是 \(2\)，故 \(a[2]\) 的状态不确定。

这个过程可以利用 bfs ，从入度为 \(0\) 的点开始搜，直到能确定状态的都被确定。

那么此时剩下的都是状态不确定的了。

此时就可以把剩下的数看作一个排列，按照上述方法判断置换环长度的奇偶性，确定答案。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read();
	vector<int> a(n+1),rd(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
		rd[a[i]]++;
	}
	vector<bool> del(n+1);//储存有哪些数的状态被确定
	queue<int> q;
	for(int i=1;i<=n;++i) {
		if(!rd[i]) {
			q.push(i);
		}
	}
	vector<int> ans;
	while(!q.empty()) {
		int x=q.front();
		q.pop();
		del[x]=true;
		ans.push_back(x);
		if(!del[a[x]] && --rd[a[a[x]]]==0) {
			q.push(a[a[x]]);
		}
		del[a[x]]=true;
	}
	bool ok=true;
	for(int i=1;i<=n;++i) {
		if(del[i]) {
			continue;
		}
		vector<int> cycle;
		for(int j=i;!del[j];j=a[j]) {
			cycle.push_back(j);
			del[j]=true;
		}
		if(cycle.size()%2) {
			ok=false;
			break;
		}
		for(int j=0;j<cycle.size();j+=2) {
			ans.push_back(cycle[j]);
		}
	}
	if(!ok) {
		puts("-1");
		return ;
	}
	printf("%lld\n",ans.size());
	sort(ans.begin(),ans.end());
	for(auto i:ans) {
		printf("%lld ",a[i]);
	}
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}