【题解】寒假训练日记

寒假给自己定的要求是 vp 后补 *2500 以下的题，有些 > 2500 但我感兴趣的题也会补。

CF2048F. Kevin and Math Class

*2500 Code

对于 \(b_x\)，找到 \(b_x\) 左侧第一个 \(l\) 使得 \(b_l < b_x\)，右侧第一个 \(r\) 使得 \(b_r < b_x\)。

那么要让 \(b_x\) 当最小值，区间最大就是 \([l+1,r-1]\)，又我们肯定是选尽可能大的区间，所以要除 \(b_x\) 时肯定是对区间 \([l+1,r-1]\) 操作。

于是建出 \((i,b_i)\) 的小根笛卡尔树，我们一定是操作笛卡尔树上的区间。

又 \(b_i \ge 2\)，所以每个区间操作不会超过 \(64\) 次。

令 \(dp[x][i]\) 表示以 \(x\) 为根的子树对应的区间，操作 \(i\) 次后区间最大值最小是多少。 \[ \begin{align} dp[x][k] = \min_{k=i+j}(\max(dp[ls[x]][i],dp[rs[x]][j],a[x]))\\ dp[x+1][k] = \min(dp[x+1][k],\left\lceil\frac{dp[x][k]}{b[x]}\right\rceil) \end{align} \] 答案是使 \(dp[rt][i]=1\) 的最小的 \(i\)。\(rt\) 是笛卡尔树的根。

时间复杂度 \(O(n\log^2w)\)，\(w\) 是值域。

题解说可以用 \(\min-\max\) 卷积优化到 \(O(n\log w)\)，但我琢磨了一下不是很会。

实测双 \(\log\) 跑了 1.1s < 2s。

CF1976D. Invertible Bracket Sequences

*2000 Code

把左括号看成 \(1\)，右括号看成 \(-1\)，求前缀和，可以作出折线图。

一段折线如果要翻转后也形成合法括号序列，需要满足两个条件：

• 两端纵坐标相等。
• 翻转后最高点不能越过 \(x\) 轴。

第一个条件即 \(sum_l = sum_r\)，第二个条件即 \(\max\limits_{l\le i\le r}sum_{i}\le2sum_l\)。

最大值可以用 ST 表或线段树维护，然后沿 \(y\) 轴做扫描线即可。注意对于同一 \(y\) 坐标，若有三个点满足 \(sum_l=sum_m=sum_r\)，且 \([l, m]\) 和 \([m,r]\) 满足要求，那么 \([l,r]\) 也满足要求。使用一个计数器累加即可。

时间复杂度 \(O(n\log n)\)。

CF1976E. Splittable Permutations

*2500 Code

这题最关键的观察：出现在 \(l[i]\)，\(r[i]\) 中的所有数的相对位置是可以唯一确定的。

• 首先对于一组 \((l, r)\)，\(l\) 肯定在 \(r\) 的左边。倒着扫描序列，每次相当于一次合并。设 \(l\) 目前所在的序列为 \(a\)，\(r\) 目前所在的序列为 \(b\)，那么合并后新序列的相对顺序一定是 \(b\) 中的元素按顺序拼接在 \(a\) 的后面。这个性质可以手玩出来。

并查集记录这个数属于哪个连通块，再用双向链表连接，就能求出这个相对顺序。

接着还有一些数没在 \(l[i]\)，\(r[i]\) 中出现过，我们考虑把它们插进去。

又一个观察：一个数 \(x\) 能插进 \(A,B\) 之间的必要条件是 \(x\le \max(A,B)\)。

• 比较显然。

于是从大到小枚举要插的数，用一个计数器统计每次有多少空可以插，乘起来就是答案。

时间复杂度\(O(n\alpha)\)。

CF2055D. Scarecrow

*2000 Code

设当前使用的时间是 \(t\)，乌鸦当前在 \(p\)。

首先离 \(0\) 最近的稻草人要移到 \(0\)，那么令初值 \(t = a[0]\)，\(p=k\)。

一个观察是：你是被你左边最近的稻草人推着走的，与此同时右边最近的稻草人可以按情况选择左移，不动，或右移来减少你转移到它（也就是被它推着走）的时间。

那么从左到右扫描每个稻草人，做出如下分类讨论：

• \(a[i]-t>p\)，即之前的时间都向左移都还在乌鸦的右边时，选择花时间继续向左，与此同时乌鸦也被它左边的稻草人推着向右，所以需要 \(t'=(a[i]-t-p)/2\)。那么 \(t=t+t'\)，乌鸦转移到 \(p=p+t'+k\)。
• \(a[i]-t\le p\) 时，分两种情况。
  • \(a[i]+t\le p\)，也就是之前的时间一直向右移也在乌鸦的左边，那就取个 \(\max\)，即 \(p=\max(p,a[i]+t+k)\)。
  • \(a[i]+t>p\)，也就是之前的时间足够右移到乌鸦右边了，此时肯定是恰好停在 $ p$ 不用花额外的时间，所以 \(p = p+k\)。

最后如果 \(p<l\)，就加上 \(l-p\)，代表最后一个稻草人把它推向终点。

时间复杂度 \(O(n)\)。

CF2057E1/E2. Another Exercise on Graphs

*2300 Code（E1）

*2500 Code1 Code2（E2）

先考虑这样一个事情：我们将原图 copy 一份，对于新图上的每条边，如果原图的边权 \(\le x\)，则赋值为 \(0\)，否则赋值为 \(1\)。那么 \(a\to b\) 在新图上的最短路为 \(w \Longleftrightarrow\) \(x\) 为原图中 \(a\to b\) 路径上第 \(w+1\) 大的边。

那么得到一个暴力做法：从小到大枚举所有的边权 \(x\)，按上述规则赋值跑最短路，直到第一个 \(w\) 满足 \(w+1\le k\)，此时 \(x\) 就是答案。

进一步地，\(x\) 每次增大都相当于把一些边（即边权等于新 \(x\) 的边）由 \(1\to 0\)，我们利用 floyd 枚举这些边的两个端点为中转点就可以很快地更新答案。具体地，更新一次是 \(O(n^2)\)，更新不超过 \(m\) 次。

至于多组询问，用 \(dis[a][b][x]\) 表示对 \(\le x\) 的边赋值为 \(0\)，否则赋值为 \(1\) 后 \(a\to b\) 的最短路，每次询问就对 \(dis[a][b][\cdot]\) 二分出第一个 \(\le k-1\) 的值对应的 \(x\) 就是答案。

由于要枚举每个边权，时间复杂度 \(O(mn^2)\)，能够通过 E1。

注意我们把一些边由 \(1\to0\) 的过程，如果对于所有边权为 \(x\) 的边 \((a,b)\)，\(dis[a][b]\) 都已经为 \(0\)，那么此次更新就是不必要的，就能省下一个 \(O(n^2)\)。

实际上，可以证明这样的更新最多进行 \(n\) 次：如果当前边 \((a,b)\) 有 \(dis[a][b]\neq0\)，那么 \(a\) 和 \(b\) 中的至少一个需要来自之前没更新过的点，而一共就 \(n\) 个点，故得证。

时间复杂度 \(O(n^3)\)，能够通过 E2。

事实上，回答询问的时候二分并不是必要的。一样是从小到大枚举边权 \(x\) 并赋值，但你只需要在 floyd 更新的时候顺便记一下就行了，细节可以阅读 jiangly 的代码。

CF2060E. Graph Composition

*1500 Code

很容易想的很复杂，实际上只需要两步：

• 把 \(F\) 的一些边断掉使得 \(F\) 的任意同一连通分量中的点都在 \(G\) 中连通。
• 把 \(F\) 的一些连通分量组合得到 \(G\)。

第一步只用枚举 \(F\) 的每条边 \(a\to b\) 然后用并查集看在 \(G\) 中 \(a,b\) 是否连通，不连通需要花费 \(1\) 的代价割掉。

第二步花费的代价一定是 \(F\) 的连通分量个数 \(-\) \(G\) 的连通分量个数。

时间复杂度 \(O(n\alpha)\)。

CF2061E. Kevin and And

*2000 Code

题目要让总和最小，一个容易想到的贪心是：每一步操作都让总和尽可能地变小，也就是每次都采取能让总和变化量最大的操作。在以下叙述中，把减少的量称为收益。

要说明这个贪心是对的，得先证明一个结论：对于一个固定的 \(a_i\)，设 \(f(j)\) 代表对 \(a_i\) 使用 \(j\) 次魔法能获得的最大的收益，那么 \(f(j)-f(j-1)\) 递减（即 \(f(j)\) 是凸的）。

• 感性证明："使用两次魔法相对于使用一次魔法" 带来的收益不可能超过 "使用一次魔法相对于不使用魔法" 带来的收益。否则此时使用一次魔法带来的收益并非是最大的。

基于这个结论，我们可以对于每个 \(i\in[1,n]\)，把所有的 \(f(j)-f(j-1),j\in[1,m]\) 记下来，排序之后选最大的 \(k\) 个值相加即最大收益。

代码实现过程中，把 \(m\) 个魔法是否使用压缩成一个状态，可以先 \(O(2^m\cdot m)\) 求出每种状态的累加效果（即按位与后的结果），再 \(O(n\cdot 2^m)\) 对每个 \(a_i\) 求出 \(f(1\sim m)\)。

时间复杂度：\(O(n2^m+nm\log nm)\)。

如果使用 std::nth_element 可以省去最后的 \(\log\)。

CF2061F1. Kevin and Binary String (Easy Version)

*2100 Code

对于串 \(\cdots011001\cdots\)，交换中间的 \(11\) 和 \(00\)，会让交换后的 \(00\) 与左边的 \(0\) 粘连，\(11\) 与右边的 \(1\) 粘连。而一旦粘连，只能一起移动，因此整块的 \(1\) 是无法跨越另一个整块的 \(1\) 的，整块的 \(0\) 也无法跨越另一个整块的 \(0\)。

这就说明了 \(s\) 要想变成 \(t\)，可以进行以下贪心：从左到右扫描，当 \(s[i]\neq t[i]\) 时，就从 \(i\) 后边找最近的整块的 \(t[i]\) 修补。

例如，\(s=001\color{Red}0\)\(1\color{Red}00\)\(101\)，\(t=00\color{Green}000\)\(1111\)。当 \(i=3\) 时，\(s[i]\neq t[i]\)，且 \(t\) 此时还有连续 \(3\) 个 \(0\)，故要从 \(s[3]\) 后边找 \(3\) 个 \(0\)。找到第一个 \(0\) 块有 \(1\) 个 \(0\)，还需要找 \(2\) 个，再往后找到下一个 \(0\) 块就恰好找到 \(2\) 个。

而 \(s=001\color{Red}0\)\(1\color{Red}00\)\(011\)，\(t=00\color{Green}000\)\(1111\) 就无法匹配上，因为往后找只能找到 \(1\) 个或 \(4\) 个 \(0\)，不能补上 \(3\) 个 \(0\) 的缺口。

具体实现时可以用容器把 \(1,0\) 的位置存起来以便快速向后查找，另有若干细节不再赘述。

时间复杂度：\(O(n)\) 或 \(O(n\log n)\)。（依据实现方式）

CF2056D. Unique Median

*2200 Code

容斥，用全集 \(\frac{n(n+1)}{2}\) 减去中位数不等的子串个数。

注意到值域很小，故枚举两个中位数中较小的那个（记为 \(x\)）。将数组中 \(\le x\) 的置为 \(-1\)，\(>x\) 的置为 \(1\) 求出前缀和 \(pre\)，那么子串 \((i,j)\) 中位数不等 \(\Longleftrightarrow\) \(pre[i-1]=pre[j]\)。

由于 \(pre[i-1]=pre[j]\) 时对应的串长定为偶数，所以不用考虑奇数长度的判断。

故我们只需要计数有多少个二元组 \((l,r)\) 满足 \(pre[l]=pre[r]\) 且区间 \([l+1,r]\) 中有 \(x\)。

一种方法是枚举 \(i=1\cdots n\)，以及一个指针 \(j\)，初始 \(j=0\)。当 \(a[i]=x\) 时，\(j\) 就跟上 \(i\) 并把路上的 \(pre[j]\) 都加进桶里，然后累加桶里 \(pre[i]\) 的数目。正确性显然，即这样两个 \(x\) 之间的 \(pre\) 值无法造成贡献。

时间复杂度 \(O(wn\log n)\)，\(w\) 为值域。

CF2056E. Nested Segments

*2500 Code

观察 \(1\)：当 \(m=0\) 时最多能向 \([1,n]\) 中填 \(2n-1\) 条线段。

• 草稿纸画几笔易得。

观察 \(2\)：当 \(m=0\) 时向 \([1,n]\) 中填 \(2n-1\) 条线段的方案数是 \(C_{n-1}\)，其中 \(C\) 为卡特兰数。

• 考虑这样一个事情：把 \([1,n]\) 当作根节点，\([1, 1],[2, 2],\cdots,[n,n]\) 当作叶节点，若 \([L,R]\) 包含 \([l,r]\) 且 \([L, R]\) 极小，就连一条边，最终连成一棵树。同时，当填满 \(2n-1\) 条线段时，这一定是一棵满位置二叉树（每个节点有 \(0\) 个或 \(2\) 个儿子），因为如果有 \(>2\) 个儿子，我们一定可以取出两个为其添加一个父亲。
• 接着套用结论：有 \(n\) 个叶子的满位置二叉树数量为 \(C_{n-1}\)。末尾的第二个参考链接附有示例。

观察 \(3\)：当 \(m\neq 0\) 时，\([1,n]\) 中仍然能填满 \(2n-1\) 条线段。

• 虽然题目预先给出了一些线段，但保证了已经给出的是好的。草稿纸再画几笔发现我们仍然能建出一个有 \(n\) 个儿子的满位置二叉树。

我们可以先把题给线段构成的树建出来（如果没有 \([1,n]\) 的话就为它添加），这时的树有些节点（设为 \(x\)）有 \(>2\) 个儿子，不妨将 \(x\) 的儿子设为 \([l_1,r_1],[l_2,r_2],\cdots[l_k,r_k]\)。对于 \(\forall i\in[1,k)\)，若 \(r_i \neq l_{i+1}\)，那么一定可以添加线段 \([r_i+1,r_i+1],[r_i+2,r_i+2],\cdots,[l_{i+1}-1,l_{i+1}-1]\) 在中间。

再设如此填充线段后 \(x\) 有 \(p\) 个儿子，我们的目标就是把这个以 \(x\) 为根的子树建成一棵满位置二叉树，而这么做的方案数恰好等价于有 \(p\) 个叶子的满位置二叉树数量，即 \(C_{p-1}\)。

于是对于每一条线段，它的贡献都是一个卡特兰数，累乘起来就是最终的方案数。

时间复杂度 \(O(n\log n)\)。

一些卡特兰数模型：Link1 Link2 Link3。

记忆：\(C_{n}=\binom{2n}{n}-\binom{2n}{n-1}\)。

CF2063F1/F2. Counting Is Not Fun

*2400 Code（F1）

*2700 Code（F2）

我们将一组 good pair \((l,r)\) 看成覆盖 \([l,r]\) 的线段，显然任何时候的任意两条线段都要么不交要么完全包含。和这篇文章的上一题及其相似，我们把具有包含关系的线段连边（对于 \([l,r]\)，若能找到极小的 \([L,R]\) 使其包含 \([l,r]\)，就在这两条线段间连一条边），会连成一棵森林。

令 \(f[i]\) 表示第 \(i\) 条线段去掉两个端点后没有被其儿子覆盖的长度。这个长度内我们可以自由填。

定理：用 \(n\) 对括号填满 \(2n\) 个位置构成平衡括号序列的方案数为 \(C_{n}\)（卡特兰数的第 \(n\) 项） 。

于是答案即为 \(\prod\limits_{i=1}^m C_{f[i]/2}\)，\(m\) 为当前添加的括号组数。

F1 中，我们可以每次添加括号后 \(O(n)\) 地去扫这个序列，求出 \(f[i]\)。

具体地，把非右括号装进栈，扫到右括号时计数弹出了多少元素。

时间复杂度 \(O(n^2)\)。

F2 需要动态地维护 \(f[i]\)，题解给出了一种平衡树做法，但离线是简单的，这里只讲离线怎么做。

倒着操作，相当于每次拿走一组括号，此时只有这条线段本身和其父亲的贡献发生了变化。具体地，设当前为第 \(i\) 条线段，父亲为第 \(fa_i\) 条线段，那么答案只需要在之前答案的基础上加上 \(-C_{f[i]/2}-C_{f[fa_i]/2}+C_{(f[fa_i]+f[i]+2)/2}\)。

快速定位到父亲是哪条线段可以用并查集，时间复杂度 \(O(n\log n + n\alpha)\)。

CF2063E. Triangle Tree

*2300 Code

草稿纸画一画，易知： \[ \begin{align} f(x,y)&= 2\min(\text{dis}(x,\text{lca}_{x,y}),\text{dis}(y,\text{lca}_{x,y}))-1 \\ &= 2\min(\text{dep}_x,\text{dep}_y)-2\text{dep}_{\text{lca}_{x,y}}-1 \end{align} \] 前提是 \(x,y\) 没有祖先关系。

这样就把贡献拆成了三部分，可以分别计算：

• \(\min(\text{dep}_x, \text{dep}_y)\)：枚举 \(x\)，则每个深度比 \(x\) 大且不在 \(x\) 子树中的 \(y\) 有 \(\text{dep}_x\) 的贡献。令 \(d_x\) 表示深度 \(\ge x\) 的节点数（可以通过一个后缀和实现），分为两种情况。
  • \(\text{dep}_x < \text{dep}_y\)：贡献为 \((d_{dep_x+1}-(sz_x-1))\times dep_x\)。
  • \(\text{dep}_x=\text{dep}_y\)：贡献为 \((d_{dep_x}-d_{dep_x+1}-1)\times dep_x\)，最后要除以 \(2\) 使无序对 \(\to\) 有序对。
• \(\text{dep}_{\text{lca}_{x,y}}\)：枚举 \(\text{lca}\)，对于当前点 \(x\)，贡献为 \(\sum_{y\in son[x]}sz_y\times (sz_x-1-sz_y)\times dep_x\)。
• \(1\)：即没有祖先关系的 \((x,y)\) 组数。对于当前点 \(x\)，贡献为 \(n-sz_x-dep_x+1\)。

第 \(2, 3\) 部分最后也需要除以 \(2\)，从而只计算有序对。

时间复杂度 \(O(n)\)。

CF2060F. Multiplicative Arrays

*2200 Code

首先注意到构造出的 \(\{a\}\) 中 \(> 1\) 的数不超过 \(16\) 个（因为 \(2^{17}>10^5\)）。

于是这个计数分为两步：

1. 算 \(>1\) 的数构成 \(x\) 有多少种可能。

2. 算剩下的 \(1\) 有多少种插空方法。

令 \(dp[i][j]\) 代表 \(i\) 个 \(>1\) 的数构成 \(j\) 的方案数。

• 初态：\(\forall i\in[2,k]\)，\(dp[1][i]=1\)。
• 转移：\(dp[i][j] = \sum\limits_{k>1} dp[i-1][\dfrac{j}{k}]\)。

令 \(ans[x]\) 代表乘积为 \(x\) 时的方案数，当 \(x=1\) 时显然为 \(n\)，当 \(x > 1\) 时： \[ ans[x]=\sum_{i=1}^{n}\sum_{j=1}^{16} dp[j][x]\binom{i}{j} \] 其中 \(i\) 为枚举的序列长度，\(\binom{i}{j}\) 代表选出 \(j\) 个 \(>1\) 的数的位置，继续化简： \[ \begin{align} ans[x]&=\sum_{j=1}^{16}\left(dp[j][x]\sum_{i=1}^{n}\binom{i}{j}\right)\\ &=\sum_{j=1}^{16}dp[j][x]\binom{n+1}{j+1} \end{align} \] 这里运用了上指标求和公式：\(\sum\limits_{i=1}^{n}\binom{i}{j}=\binom{n+1}{j+1}\)，可以借助杨辉三角记忆。

虽然 \(n\) 比较大，但 \(\binom{n+1}{j+1}\) 可以用定义 \(O(\log k)\) 求得，故总时间复杂度 \(O(k\log^2k)\)。

CF2007E. Iris and the Tree

*1800 Code

编号是 dfs 序，说明任意一条边都恰好被两条 \(i\to i+1\) 的路径经过（初次遍历时至上而下一条，回溯时至下而上一条）。

我们可以暴力地把每条 \(i\to i+1\) 的路径经过的点记录下来，由于总长度是 \(2n\)，所以是线性的。

当我们给一条边赋值后，我们找到这条边对应的两条路径，此时这两条路径的边权和有两种情况：

• 这条路径上仍然有边权不确定的点。此时可以把剩余的权值全部分配给那条边权不确定的边。
• 这条路径上所有边都被赋值了。此时边权和是固定的。

我们可以记录两个信息以快速计算贡献，分别是已经赋值过的权值和 \(add\) 以及未被全部赋值的路径条数 \(cnt\)。

此时第二种情况和第一种情况的已赋值部分等价于 \(2\cdot add\)，第一种情况的未赋值部分等价于 \(cnt\cdot(w-add)\)。

时间复杂度 \(O(n\log n)\)。带 \(\log\) 是因为使用了 std::set 来辅助计算 \(cnt\)。

CF2007F. Eri and Expanded Sets

*2300 Code

连续意味着排序后相邻两项的差是 \(1\)，这引导我们思考差分数组。

结论：对于一个有序序列 \(\{a\}\)，它不能再进行 expand 当且仅当它的差分数组 \(\{b\}\) 全为奇数且相同。换句话说，\(\{a\}\) 是公差为奇数的等差数列。

• 若 \(b_i=a_{i+1}-a_i\) 为偶数，则一定有 \(c=\frac{a_i+a_{i+1}}{2}\in(a_i,a_{i+1})\) 可以加进 set 里。
• 若存在相邻两项 \(b_i,b_{i+1}\) 为奇数但不同，则 \(b_i+b_{i+1}=a_{i+2}-a_{i}\) 为偶数，且 \(c=\frac{a_{i+2}+a_i}{2}\in(a_i,a_{i+1})\cup(a_{i+1},a_{i+2})\) 不在序列里，可以再 expand。

进一步地，假定 \(g=\gcd\limits_{i\in[1,n)}(|a_{i}-a_{i+1}|)\)，\(\{a\}\) 的公差为 \(d\)，则 \(d\) 一定是 \(g\) 除以 \(2\) 的若干次幂得到。具体地，\(d=\dfrac{g}{\text{lowbit}(g)}\)。

• 因为任意两项的差要是公差 \(d\) 的倍数，故 \(d\) 是相邻两项差的 \(\gcd\) 的因数 。而 \(g\) 能再分的前提是 \(g\) 是偶数，故 \(g\) 不断除以 \(2\) 直到为奇数就得到 \(d\)，写成公式就是上面那样。

还需要注意的是这里引入了 \(\gcd\)，根据其辗转相减的性质，结论对于无序数组依然成立。

回到题目的要求，连续即 \(d=1\)，即：

\[ d=\dfrac{g}{\text{lowbit}(g)}=1\Longrightarrow g=\text{lowbit}(g)\Longrightarrow g=0 \cup g=2^k,k\ge 0 \]

转化为求 \(\{b\}\) 有多少个子区间的 \(\gcd\) 为 \(0\) 或 \(2\) 的幂。

枚举左端点 \(L\)，二分找到第一个右端点 \(R\) 满足 \(\underline{\ }\text{builtin}\underline{}\text{popcount}\left(\gcd\limits_{i\in[L,R]}b_i\right)=1\)。则区间 \([L,R], [L,R+1],[L,R+2],\cdots,[L,n]\) 的 \(\gcd\) 均为 \(2\) 的幂次。这是因为 \(2\) 的幂次只有因数 \(2\)，与任何数做 \(\gcd\) 也只能得到 \(2\) 的幂次。

还是通过二分找到最后一个右端点 \(R\) 满足 \(\gcd\limits_{i\in[L,R]}b_i=0\)，则区间 \([L,L],[L,L+1],[L,L+2],\cdots,[L,R]\) 的 \(\gcd\) 均为 \(0\)，原因显然。

区间 \(\gcd\) 可以用 ST 表实现，时间复杂度 \(O(n\log n)\)。

CF2062D. Balanced Tree

*2200 Code

操作是：选定一个根，再让一个点的子树 \(+1\)。

对于一条边，我们只会让它一侧的所有节点 \(+1\)（因为两侧都加等价于整棵树加，是没有意义的）。

想象所有点都已经固定点权了，此时肯定是让点权小的一侧的所有点权 \(+1\)。边的决策取决于两侧的节点，不妨先随意选定一个根，进行至下而上地贪心。

设 \(f[x]\) 为节点 \(x\) 的答案，并初始化一个 \(delta=0\) 代表全局 tag。对于当前节点 \(x\)，若为叶子，选 \(L[x]\) 肯定不劣；否则有两种情况：

• \(\forall y\in son[x]\)，\(f[y]\le r[x]\)。此时选 \(\max(l[x],\max\limits_{y\in son[x]} f[y])\) 肯定最优。因为可以让某一个儿子所在的子树变大，儿子之间互不影响。
• \(\exists y\in son[x],f[y]>r[x]\)。此时节点 \(x\) 只能选 \(r[x]\)，为了让所有节点权值一样只能让 \(x\) 沿着根方向的子树 \(+1\)。并且对于每个儿子所在的子树，造成的贡献是累加的，即 \(delta \leftarrow delta + \sum\limits_{y\in son[x],f[y] > r[x]} (f[y]-r[x])\)。

答案即 \(f[rt]+delta\)，时间复杂度 \(O(n)\)。

CF2033G. Sakurako and Chefir

*2200 Code

对于一组询问 \((v,k)\)，我们直接跳到 \(v\) 的 \(k\) 级祖先（设为 \(x\)）一定不劣。

那么询问等价于找 \(x\) 的子树中距 \(v\) 最远的点。

这个最远的点一定是 \(x\) 的子树的两个直径端点之一。

问题转化为对树上的每个点 \(x\)，求其子树的直径的两个端点。

这仍然是一个套路化的问题，回顾一下做法：

• 至下而上考虑，设当前考虑的节点为 \(x\)。
• 若 \(x\) 为叶子，两个直径端点都是它自身。
• 若 \(x\) 恰有一个儿子 \(y\)，考虑 \(x\) 是否能与 \(y\) 的两个端点之一来作为新的直径，不能就直接继承 \(y\) 的答案。
• 若 \(x\) 有两个儿子 \(y_1,y_2\)，答案为两种情况取 \(\max\)：
  • 继承自 \(y_1\) 或 \(y_2\)。
  • 穿过 \(x\) 将两段拼起来。此时新的直径端点肯定有一个来自 \(y_1\) 的两个端点之一，另一个来自 \(y_2\) 的两个端点之一。
• 若 \(x\) 有 \(> 2\) 个儿子，按上一种情况每次合并两个子树，直到合并完为止。

时间复杂度 \(O(n\log n)\)。

CF1993D. Med-imize

*2200 Code

答案具有二分性，设二分出的答案为 \(mid\)。

中位数套路：\(\forall i\in[1,n]\)，令 \(b[i]=\begin{cases}1&,a[i]\ge mid \\ -1&,a[i]<mid\end{cases}\ \)，则 \(\sum b[i]>0 \Longleftrightarrow mid\le median(a)\)。

题目转化为：给定 \(\{b\}\)，每次任选一个长为 \(k\) 的段删掉，直到不能删为止，剩下数的和是否 \(>0\)。

这里给出其中一种 dp 方案。

令 \(dp[i][j]\) 表示前 \(i\) 个数选了 \(j\) 个长为 \(k\) 的段删去后，剩下数和的最大值。

则 \(dp[i][j] = \max(dp[i-1][j]+b[i],dp[i-k][j - 1])\)，答案为 \(dp[n][\left\lfloor\frac{n-1}{k}\right\rfloor]\)。

考虑到 \(0\le i-jk\le k \Longrightarrow j\in\left[\left\lfloor\dfrac{i-1}{k}\right\rfloor,\left\lfloor\dfrac{i}{k}\right\rfloor\right]\)，即 \(j\) 只有两种取值。

故不妨令 \(dp[i][j=0/1]\) 表示前 \(i\) 个数选了 \(\left\lfloor\dfrac{i-1}{k}\right\rfloor+j\) 个长为 \(k\) 的段删去后，剩下数和的最大值。

使用记忆化搜索转移，时间复杂度 \(O(n\log w)\)，\(w\) 是值域。

官方题解里是另一种 dp，我花了半个小时仍未完全理解，希望有生之年能够参悟。

CF1993F1/F2. Dyn-scripted Robot

*2400 Code（F1）

*2800 Code（F2）

我们假定一个在没有墙的二维平面中移动的机器人称作 \(B\)，题中的机器人称作 \(A\)。由于 \(B\) 相比 \(A\) 取消了墙的限制，移动序列自然不会改变。

结论：\(A\) 回到原点的次数 \(\Longleftrightarrow\) \(B\) 经过点 \((x,y),\begin{cases}x\equiv 0\pmod{2w} \\ y\equiv 0 \pmod{2h} \end{cases}\) 的次数。

• 先考虑只存在沿 \(y\) 轴方向的移动，当 \(A\) 撞到 \(y=h\) 后，\(A,B\) 运动轨迹沿 \(y=h\) 轴对称；而 \(A\) 再撞到 \(y=0\)（\(B\) 撞到 \(y=2h\)）后，二者运动方向恢复一致。\(x\) 轴方向的运动同理，外推后不难得出该结论。

故只需研究 \(B\) 的运动即可。设 \(x_i\ (i\in[1,n])\) 表示 \(B\) 从 \((0,0)\) 开始，经过 \(i\) 次移动后的横坐标（在 \(\bmod 2w\) 同余系下）; \(y_i\ (i\in[1,n])\) 表示 \(B\) 从 \((0, 0)\) 开始，经过 \(i\) 次移动后的纵坐标（在 \(\bmod 2h\) 同余系下）。

假设 \(B\) 已经执行了完整的移动序列 \(i\in[0,k)\) 次，并额外移动了 \(j\in[1,n]\) 次，那么坐标为 \((ix_n+x_j,iy_n+y_j)\)。题目转化为求有序对 \((i,j)\) 的数目，满足：

\[ \begin{cases} x\equiv 0 \pmod{2w} \\ y\equiv 0 \pmod{2h} \end{cases} \Longrightarrow \begin{cases} ix_n+x_j\equiv 0 \pmod{2w} \\ iy_n+y_j\equiv 0 \pmod{2h} \end{cases} \]

对于 F1，将式子变形，得到：

\[ \begin{cases} x_j\equiv -ix_n \pmod{2w} \\ y_j\equiv -iy_n \pmod{2h} \end{cases} \]

我们可以把执行一次移动序列经过的点的坐标存到一个 std::map 里，然后枚举 \(i\in[0,k)\)，查一下 std::map 中点 \((-ix_n,-iy_n)\) 的值即可。时间复杂度 \(O(k\log n)\)。

对于 F2，将式子变形，得到：

\[ \begin{cases} ix_n\equiv -x_j \pmod{2w} \\ iy_n\equiv -y_j \pmod{2h} \end{cases} \]

在这个方程组中，除了 \(i\) 均为已知，于是可以枚举 \(x_j\)，用中国剩余定理解 \(n\) 遍即可。在此之前，还需要把方程转化为 \(x\equiv a\pmod{p}\) 的标准形式。

由于 \(a\) 在 \(\bmod p\) 下的逆元仅在 \(a,p\) 互质时存在，故令 \(g=\gcd(2w,x_n)\)，则：

\[ \begin{align} ix_n&\equiv -x_j \pmod{2w}\\ i\cdot\frac{x_n}{g}&\equiv -\frac{x_j}{g}\pmod{\frac{2w}{g}}\\ i &\equiv -\frac{x_j}{g}\left(\frac{x_n}{g}\right)^{-1}\pmod{\frac{2w}{g}} \end{align} \]

显然当 \(g \nmid x_j\) 时方程无解。另一个方程组同理。

对于一组 \((x_j,y_j)\)，用 CRT 解出最小的 \(i\) 后，问题转化为 \(i,i+M,i+2M,\cdots\) 中有几个在 \([0,k-1)\) 范围内，答案是 \(\dfrac{k-1-i}{M}+1\)。

时间复杂度 \(O(n\log w)\)。

CF1972D. Reverse Card (Hard Version)

*2200 Code

题目要求满足 \(a\in[1,n]\)，\(b\in[1,m]\)，\((a+b)\mid b\cdot\gcd(a,b)\) 的有序对 \((a,b)\) 的数量。

令 \(d=\gcd(a,b)\)，\(a=pd\)，\(b=qd\)，则 \(\gcd(p,q)=1\)。代入得： \[ \begin{align} a+b&\mid b\cdot\gcd(a,b)\\ \to (p+q)d&\mid qd^2 \\ \to \quad \ p+q&\mid qd\\ \to \quad\ p+q&\mid d \end{align} \] 最后一步是因为 \(\gcd(p,q)=1 \to \gcd(p+q,q)=1\)。

又因为：

\[ \begin{align} p+q\mid d \to p+q\le d\to p\le d=\dfrac{a}{p}\le \dfrac{n}{p} \end{align} \]

于是 \(p^2 \le n \to p\in[1,\sqrt{n}]\)，同理 \(q\in[1,\sqrt{m}]\)。

\(O(\sqrt{nm})\) 枚举 \(p,q\)，当 \(\gcd(p,q)=1\) 时，贡献等价于有多少 \(d\) 满足 \(p+q\mid d\) 且 \(d\le \min(\dfrac{n}{p},\dfrac{m}{q})\)，即 \(\left\lfloor\dfrac{\min(\dfrac{n}{p},\dfrac{m}{q})}{p+q}\right\rfloor\)。

时间复杂度 \(O(n\log n)\)。

CF1824B2. LuoTianyi and the Floating Islands (Hard Version)

*2300 Code

规定有人的点称为黑点，到所有黑点距离和最小的点称为目标点。

结论：目标点构成一个连通块。

• 比较显然。

结论：当 \(k\) 为奇数时，答案为 \(1\)。

• 对于任意一个有奇数个黑点的局面，假定我们已经找到了一个目标点 \(x\)。若存在 \(x\) 的一个邻居 \(y\) 也是目标点，那么 \(x\to y\) 移动的过程中理应没有额外贡献，换句话说边 \((x,y)\) 两侧黑点数目相同。此时黑点个数定为偶数，矛盾。故对于任意一个奇数个黑点的局面有且仅有一个目标点。

接下来考虑将点的贡献放到边上，好处是目标点构成连通块，边的数量总是目标点数量 \(-1\)，而且边的贡献容易计算。

当 \(k\) 为偶数时，根据上述分析，一条边当且仅当两侧黑点数目相同时有贡献，故贡献为两侧各选 \(\dfrac{k}{2}\) 个黑点的方案数。

任选根计算出 \(sz[x]\) 为子树大小，那么答案即 \(\dfrac{\sum\limits_{x=1}^{n}\sum\limits_{y\in son[x]}\dbinom{sz[y]}{\dfrac{k}{2}}\dbinom{n-sz[y]}{\dfrac{k}{2}}}{\dbinom{n}{k}}+1\) 。

时间复杂度 \(O(n)\)。

CF1989D. Smithing Skill

*1900 Code

首先，不同 \(c_j\) 互不影响。其次，对于一个 \(c_j\)，肯定是选满足 \(c_j\ge a_i\) 的武器中 \(a_i-b_i\) 最小的武器，并不断地合成再焚毁直到 \(c_j < a_i\) 为止。

考虑阈值分治，令 \(A=\max a_i\)，可以先对每个 \(i\in[1,A]\) 预处理出 \(res[i]\) 表示 \(i\) 个矿石能够获得的最大经验点数；而对于 \(c_j > A\) 的询问，用最小的 \(a_i-b_i\) 处理直到 \(c_j \le A\)，就能直接查表查到 \(res[c_j]\)。

其中 \(res[i]\) 的预处理仍然不简单，我们可以定义一个辅助数组 \(d[i]\) 表示所有 \(a_i \le i\) 的武器里面 \(a_i-b_i\) 的最小值。在此基础上，有递推 \(res[i]=2+res[i-d[i]]\)。

时间复杂度 \(O(n+w+m)\)，\(w\) 为值域。

CF1972E. Fenwick Tree

*2300 Code

首先要知道树状数组的结构是怎么样的，这里引用题解的一张图。

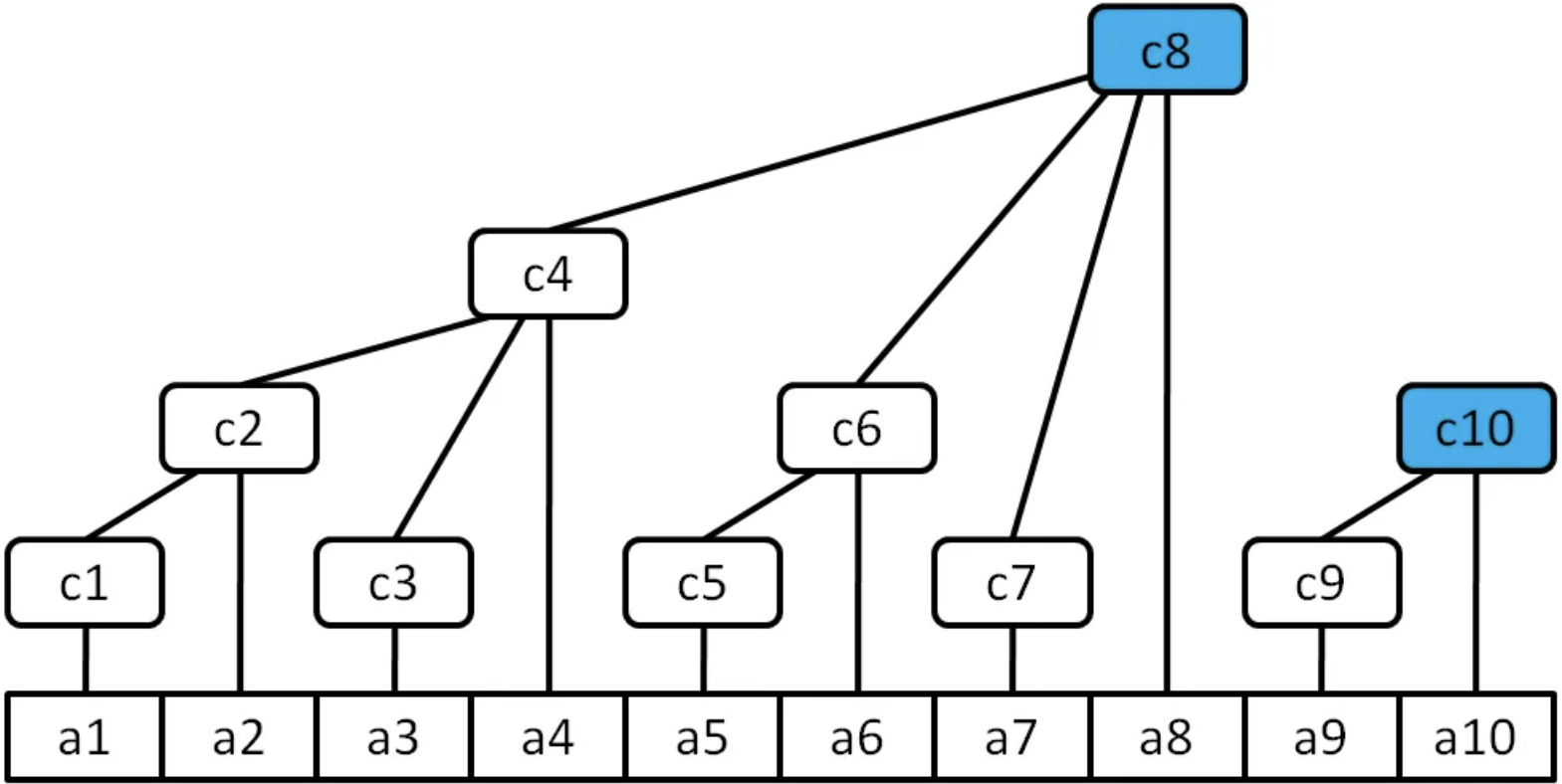
其中 \(c_1,c_2,\cdots c_{10}\) 就是迭代一次后的数组，即 \(f^{1}(a)\)。

故每次迭代相当于把上一次迭代后的数组作为叶子，再向上合并一遍。

我们考虑对每个 \(c_i\)，把它的贡献从它的祖先中除去。

例如，当 \(k=1\) 时，对于 \(c_1\)，要把 \(c_1\) 从 \(c_2,c_4,c_8\) 中除去，此时系数显然都是 \(1\)。（系数即 "减去几倍的 \(c_1\)"）

当 \(k=2\) 时，\(c_2\) 在第一次迭代的基础上再累加了一遍 \(c_1\)，系数是 \(1+1=2\)；\(c_4\) 累加了 \(c_2\)，系数是 \(1+2=3\)；\(c_8\) 累加了 \(c_4\)，系数是 \(1+3=4\)。

当 \(k=3\) 时，\(c_2\) 再累加一遍 \(c_1\)，系数是 \(2+1=3\)；\(c_4\) 累加 \(c_2\)，系数是 \(3+3=6\)；\(c_8\) 累加 \(c_4\)，系数是 \(4+6=10\)。

可以发现，对于相同的 \(k\)，系数只和向上爬升的层数有关，列成一个表。

\(k=1\to 1,1,1,1,1,\cdots\)

\(k=2\to 2,3,4,5,\cdots\)

\(k=3\to 3,6,10,\cdots\)

\(k=4\to 4,10,\cdots\)

将这个三角形摆正，可以发现就是杨辉三角。

其中，第 \(i\) 行第 \(j\) 项表示 \(k=i\) 时向上爬升 \(j\) 层需要减去的系数，组合数写出来就是 \(\dbinom{i+j-1}{j}\)。

由于树状数组不超过 \(\log n\) 层，故时间复杂度 \(O(n\log n)\)。

CF1996G. Penacony

*2200 Code1 Code2

solution1：对于一对朋友 \((a,b)\)，他们之间有且仅有两条路径，并且这两条路径构成一个环。因此最为关键的观察是 '"只要钦定某一条边是断开的，那么每一对朋友间的路径就是唯一的"。

建一棵 \(n\) 个点的线段树，每个位置的值代表对应的道路被几对朋友占用了。一开始，先将所有 \([a,b)\) 区间 \(+1\)。从左到右枚举每条边并钦定为断开，如遇到左端点就将 \([1,a),[b,n]+1\)，\([a,b)-1\)；如遇右端点就将 \([1,a),[b,n]-1\)，\([a,b)+1\)。每次修改完查询 \([1,n]\) 中 \(0\) 出现的次数就是非必须保留的道路数目。

由于整个修改过程线段树保存的值非负，故 \(0\) 出现的次数等价于最小值出现的次数。

solution2：将这 \(n\) 个点 \(n\) 条边看成一个 \(n\) 边形，对于一对朋友 \((a,b)\)，在 \(a,b\) 间连对角线。

断言：对于任意两条边，如果它们被相同的对角线集合覆盖，那么这两条边可以删去。

• 你可以想象每条对角线都有正反面，正面对应多边形上的边和反面对应多边形上的边被认为是不同的。就一对朋友关系而言，你能且仅能选择两段其一。

对于每条对角线，我们不妨把其任一侧的所有边异或上一个固定的值。

利用差分和前缀和，就能 \(O(n)\) 求出每条边在 “染色” 后的权值。此时两条边权值相同就等价于被相同的对角线集合覆盖了。

最后，用一个 std::map 统计出现次数最多的权值即可。

两种方法时间复杂度均为 \(O(n\log n)\)，后者常数小很多。

CF1983E. I Love Balls

*2300 Code

数学题。令 \(special=\dfrac{\sum_{i=1}^{k}v_i}{k}\)，\(normal=\dfrac{\sum_{i=k+1}^{n}v_i}{n-k}\)，分别表示特殊球和普通球的期望价值。

考虑将 \(k\) 特殊球插进 \(n-k+1\) 个普通球的 gap 里面，每个 gap 可以放多个特殊球，这么建立模型的好处是你选中一个 gap 就拿完这个 gap 里的所有球，符合特殊球的机制。

Alice 会选中 \(\left\lceil\dfrac{n-k+1}{2}\right\rceil\) 个 gap，每个 gap 里特殊球期望有 \(\dfrac{k}{n-k+1}\) 个，故 Alice 选中特殊球价值的期望总和是 \(\dfrac{\lceil\frac{n-k+1}{2}\rceil \cdot k}{n-k+1}\cdot special\)。

而 Alice 作为先手会选中 \(\left\lceil\dfrac{n-k}{2}\right\rceil\) 个普通球，故他选中普通球价值的期望总和是 \(\left\lceil\dfrac{n-k}{2}\right\rceil\cdot normal\)。

根据期望的线性性， 上述两个式子相加就是 Alice 的答案。Bob 的答案即所有球的价值总和减去 Alice 的答案。

时间复杂度 \(O(n)\)。

CF1983F. array-value

*2500 Code

二分答案，设二分出的答案是 \(mid\)，若至少有 \(k\) 个区间的 value \(\le mid\)，就往小二分，否则往大二分。

问题转化为判断求有多少个区间的 value \(\le mid\)。

不妨枚举右端点 \(r\)，此时只需找到最大的 \(l\) 满足 \(a_l \oplus a_r \le mid\)，那么左端点位于 \([1,l]\) 内构成的区间均满足条件。

这是个经典的问题，使用一个 trie 就能维护，步骤如下：

• 对每个 trie 树上的节点 \(p\) 维护一个 \(mx[p]\) 存储经过这个点的值中下标最大值。
• 假设当前对 \(a_i\) 进行查询，我们要返回一个最大的 \(j\) 满足 \(a_j\oplus a_i \le mid\)。从大到小枚举每一位，设 \(a_i\) 当前位为 \(x\)，\(mid\) 当前位为 \(m\)。
  • 若 \(m=0\)，为了满足 \(\le mid\) 的条件，\(a_j\) 这一位应和 \(x\) 相同，故只能向 \(x\) 的方向走。
  • 若 \(m=1\)，那么两边都可以走：如果向 \(x\) 一侧走，之后无论怎么走得到的 \(a_j\) 都会满足 \(a_j \oplus a_i \le mid\)，故直接累加 \(x\) 一侧的 \(mx[p]\)，并转而走向 \(x\) 的对侧。
• 最后走到底得到的 \(a_j\) 一样满足条件，故答案还要和末尾节点的 \(mx[p]\) 取 \(\max\)。

时间复杂度 \(O(n\log^2w)\)，\(w\) 为值域。

CF2004F. Make a Palindrome

*2600 Code

结论：两种操作对最小操作次数的影响等价，即任选其中一种操作或两种操作都用得到的答案相同。

• 考虑对于一个 \(\{b\}\)，如何计算 \(f(b)\)。设 \(\{b\}\) 中第一个元素是 \(b_1\)，最后一个是 \(b_n\)。首先若 \(b_1=b_n\)，可以将它们从序列中拿掉，直到 \(b_1 \neq b_n\)。此时如果使用分裂操作肯定是选择将 \(b_1,b_n\) 中较大的那个分解成较小的那个，不妨设 \(b_1 < b_n\)，则相当于耗费一次操作将 \(b_1,b_n\) 去掉并在右侧添加一个 \(b_n-b_1\)。此时若 \(b_n-b_1 \neq b_2\)，那么此次分裂只是单纯把序列元素个数减少了一个，合并操作同样能做到。若 \(b_n-b_1=b_2\)，说明此时可以额外将最左侧的 \(b_2\) 和最右侧的 \(b_n-b_1\) 去掉，一次操作相当于减少了两个元素；但移项可知 \(b_1+b_2=b_n\)，说明最开始我们如果在左侧用一次合并生成 \(b_1+b_2\) 再和右边的 \(b_n\) 抵掉，也是减少了两个元素。于是分裂和合并操作是等价的。

接下来我们只讨论合并操作。在最极端的情况下，将长为 \(n\) 的序列变成回文需要 \(n-1\) 次操作，考虑什么情况能减少操作次数。

结论：对于一个序列，如果其某一个非空前缀和某一个非空后缀的元素和相同，就能减少一次操作。

• 设序列长为 \(n\)，若 \([1,l]\) 和 \([r,n]\) 的元素和相同，说明从两端移去数的过程进行到只剩 \(\sum\limits_{i=1}^{l-1}a_i,a_l,a_{l+1},\cdots,a_{r-1},\sum\limits_{i=r}^{n}a_i\) 或 \(\sum\limits_{i=1}^{l}a_i,a_{l+1},\cdots,a_{r-1},a_r,\sum\limits_{i=r+1}^{n}a_i\) 时，头两个元素合并或后两个元素合并就能额外减少一个元素，换句话说少用了一次操作，并且操作后序列的结构和操作前一致，可以继续寻找最近的非空前缀和最近的非空后缀。

特别地，找到的非空前缀和非空后缀可以相交，如何理解？若有 \([1,l]\) 和 \([r,n]\) 元素和相等但 \(l>r\)，说明一定有 \([1,r]\) 和 \([l,n]\) 元素和相等而中间 \([r,l]\) 的部分共用，此时 \([r,l]\) 一定构成回文串而不用删掉。

回到原本的问题上来，我们要计算 \(\{a\}\) 所有非空子数组 \(\{b\}\) 的 \(f(b)\) 之和。假若我们在 \(\{a\}\) 中发现了一组 \([l_1,r_1]\)，\([l_2,r_2]\) 元素和相等，那么这两段如果要作为前后缀只能是对 \([l_1,r_2]\) 有 \(-1\) 的贡献，对其它区间都没有贡献，故对整个序列的贡献就是 \(-1\)。

故题目转化为求 \(\{a\}\) 中有多少对非空子区间相等，枚举每个区间存到 std::map 里统计即可。

时间复杂度 \(O(n^2\log n)\)。

CF1821D. Black Cells

*1900 Code1 Code2

solution1：通过观察能得出结论：选择长度 \(\ge 2\) 的区间一定不劣。

• 随便举个例子：假设 \(k=4\)，对于 \([1,1]\) 和 \([4,7]\)，选择两个区间最少消耗 \(10\) 次操作，如果只选 \([4,7]\) 则最少只消耗 \(9\) 次。但若是 \([1,2]\) 和 \([4,7]\)，无论选择两个区间还是只选 \([4,7]\)，最少都是消耗 \(9\) 次操作。

于是我们记录 \(\text{one}\) 和 \(\text{sum}\) 分别代表长为 \(1\) 的区间个数和长度 \(\ge 2\) 的区间的长度和。从左到右扫，分 \(\text{sum}\ge k\) 和 \(\text{sum}+\text{one}\ge k\) 讨论即可。

时间复杂度 \(O(n)\)。

solution2：显然选长度尽可能大的区间更优，故使用反悔贪心。

压入堆中的是已经选择的区间的长度。每当堆中元素和 \(\ge k\)，就把最小的元素弹出来。

时间复杂度 \(O(n\log n)\)。

CF1821E. Rearrange Brackets

*2100 Code

题意差评，一堆能让人误会的地方。

首先，对于给定的平衡括号序列，得到最小 cost 的方式是每次移除最右侧的相邻括号对。

对于两对括号 \(A,B\)，如果 \(A\) 包含 \(B\)，就连一条 \(A\to B\) 的边，建出括号森林。不妨设节点 \(1\) 是虚根，这样得到一棵括号树。

那么移除节点 \(x\) 的代价就是 \(x\) 的非 \(1\) 祖先数目。换句话说，对于任意一个点，它子树内的每个点都有 \(1\) 的贡献，即这组括号序列的最小 cost 是 \(\sum\limits_{i=2} sz[i]-1\)。

考虑移动一个括号，可行的移动方式是 \(A(B)C\to A()BC\)，这等价于把一个点 \(x\) 的儿子接到父亲上，再把 \(x\) 删去。不难发现这个过程是无序的（即只要删除的点集是一样的得到的括号树就一样），你只要将 \(sz[i]-1\) 排序后选最大的 \(k\) 个删去就行。

时间复杂度 \(O(n\log n)\)。\(k\) 的范围十分诈骗。

CF2022E2. Billetes MX（Hard Version）

*2600 Code

结论：对于一个 beautiful 的 \(n\times m\) 网格，一定存在长为 \(n\) 的序列 \(\{X\}\) 和长为 \(m\) 的序列 \(\{Y\}\) 满足 \(a[i][j]=X[i]\oplus Y[j]\)。

• 容易说明，对于一个 beautiful 的网格，我们将任意一行异或上任意一个数后得到的新网格仍然 beautiful。于是我们进行如下操作：将每一行都异或上那行的第一个数，每一列都异或上那列的第一个数。这样我们得到了一个第一行、第一列全为 \(0\) 的网格，它仍然 beautiful。
• 此时 \(\forall i\in[2,n],j\in[2,m]\)，有 \(a[i][j] \oplus a[1][j]\oplus a[i][1] \oplus a[1][1]=0\)，由于后三项均为 \(0\)，则 \(a[i][j]=0\)。我们取第一列为序列 \(\{X\}\)，第一行为序列 \(\{Y\}\)，由 \(a[i][j]\) 在异或完 \(X[i]\) 和 \(Y[j]\) 后为 \(0\)，可知 \(a[i][j]=X[i]\oplus Y[j]\)。

那么，\(a[i][j]\) 给定意味着 \(X[i] \oplus Y[j]\) 给定，我们建立一个图论模型：一个 \(n+m\) 个点的图，点 \(1\sim n\) 代表对应的行，点 \(n+1\sim n+m\) 代表对应的列，给定 \(a[i][j]\) 就连一条 \(i \to n+j\) 边权为 \(a[i][j]\) 的边。

根据异或的性质，在这个图中所有的环都要满足 "环上的边权异或和为 \(0\)"。若不满足，答案就是 \(0\)。否则方案数是什么呢？考虑一个没填数的格子，不妨设它的坐标是 \((r, c)\)，将它填上相当于将点 \(r\) 和点 \(n+c\) 连起来了，分两种情况：

• 连之前 \(r\) 和 \(n+c\) 就在一个连通块里了。此时新加进的这条边能构成一个新环，由于一个环上的边异或和要为 \(0\)，这条新边权值自然是固定的，答案 \(\times 1\)。
• 连之前 \(r\) 和 \(n+c\) 不在一个连通块中。此时新加进的这条边不组成任何一个环，边权就能取任何一个 \([0,2^{30}-1]\) 中的值，故答案 \(\times 2^{30}\)。

也就是说，对于当前的一个局面，有 \(cnt\) 个连通块，且所有环都满足边权异或和为 \(0\)，答案就是 \(2^{30\cdot cnt}\)。

连通块数目用并查集容易维护，只用考虑如何每次修改后都 check 异或和为 \(0\) 的条件。

实际上这个问题同样能用并查集维护：我们对图上每个点 \(x\) 记录一个 \(g[x]\) 表示 \(x\) 到它所在连通块的根的距离（这个根也就是并查集里 find 得到的点）。那么并查集 merge 的时候如果发现 \(x,y\) 在一个连通块中且 \(g[x]\oplus g[y] \neq w\)，就说明我们发现了异或和 \(>0\) 的环。

\(g[x]\) 则通过以下操作维护：

• find 函数回溯时 \(g[x] =g[x]\oplus g[fa[x]]\)。
• merge 时假定 \(fa[rt_y]=rt_x\)，则 \(g[rt_y]=(g[x] \oplus g[y]\oplus w)\)。

给一幅图帮助理解，不再赘述。

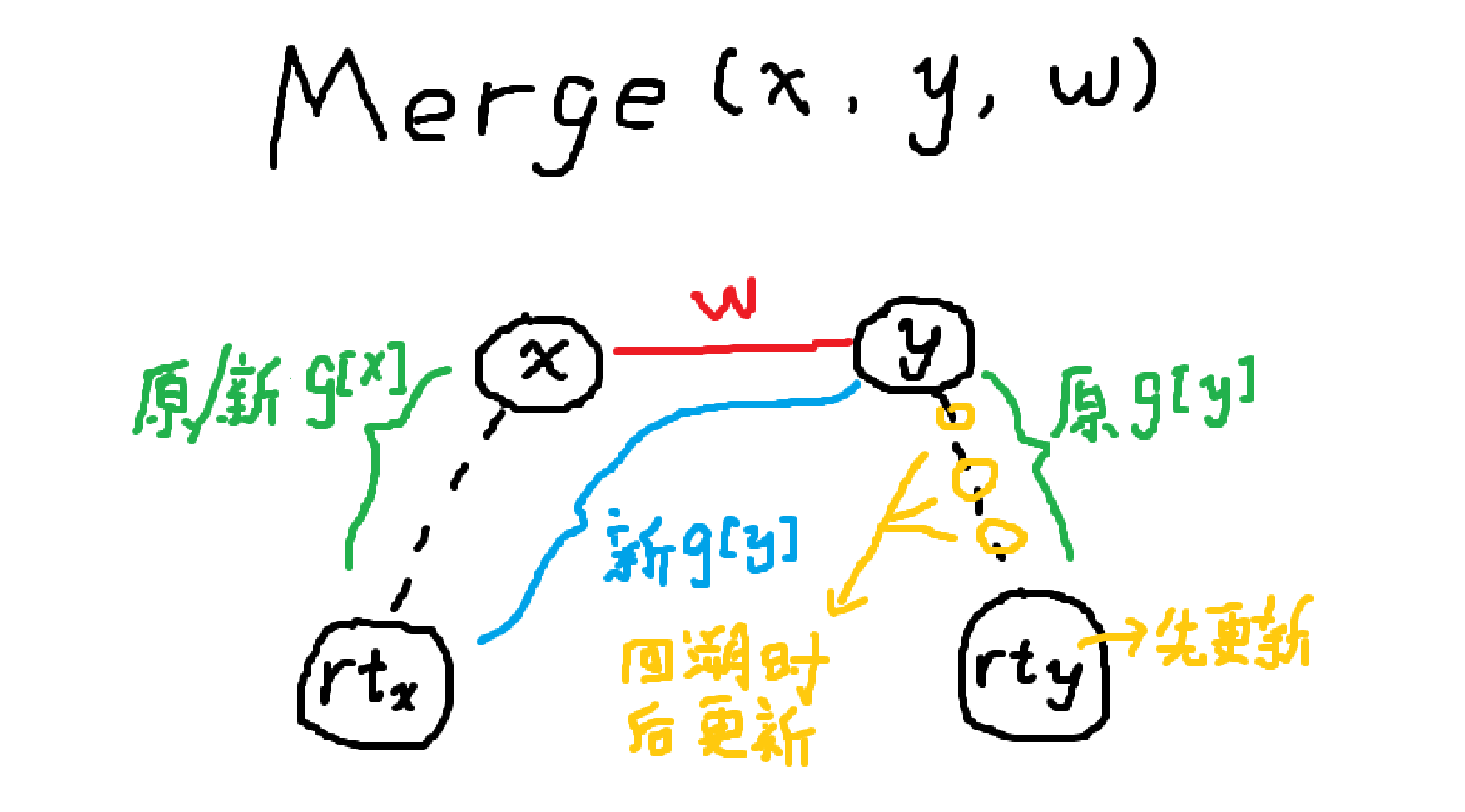
时间复杂度 \(O((n+q)\alpha)\)。

CF1972F. Long Way to be Non-decreasing

*2800 Code

建图：\(\forall i\in [1, m]\)，\(i\to b_i\)。

问题转化为：求最小的 \(k\)，使得每个 \(a_i\) 最多能在图上走 \(k\) 步，得到的序列单调不降。

容易发现答案单调，于是二分答案，设二分出的答案是 \(mid\)。

考虑一个贪心，对于第一个数而言，肯定是选 \(mid\) 步内的权值最小点；第二个数肯定是选 \(mid\) 步内权值大于等于第一个数的最小点，以此类推。我们从小到大枚举权值判定能否走到，若能走到，就跳到下一个数；否则继续往大了枚举。

具体地，我们用一个三元组 \((S,T,mid)\) 表示一个判定：判定 \(S\) 走不超过 \(mid\) 步是否能走到 \(T\)。 \(T\) 显然单调不降，于是我们只需判定 \(O(m)\) 次。

判定很简单，只是需要一些码力。首先 \(i\to b_i\) 能得到一棵基环内向树，两点间的距离分为环上的一段和子树的一段，维护是朴素的。记录每个点属于哪个环对应的子树以及深度，就能 \(O(1)\) 得到距离，再和 \(mid\) 比较即可。无解情况是：

1. \(S, T\) 不在同一棵子树内并且 \(T\) 不在环上。
2. \(S,T\) 在同一棵子树内但 \(T\) 深度大于 \(S\) 或二者不是祖先关系。

时间复杂度 \(O(n\log m)\)。

CF1969D. Shop Game

*1900 Code

Bob 会从 Alice 选的物品里选 \(k\) 个 for free，那他肯定会选 \(b[i]\) 最大的 \(k\) 个。

我们不妨将物品按 \(b[i]\) 降序排序，这样相当于我们要选一个长至少为 \(k\) 的子序列，然后把长为 \(k\) 的前缀舍去。

这样的好处是要舍去的物品和剩下 Bob 要从 Alice 手里买来的物品有了分界线。我们枚举这个分界线，分界线前我们选 \(k\) 个舍去，贪心来讲一定是选 \(a[i]\) 最小的 \(k\) 个；分界线后我们要获得最大的利润，一定是选所有 \(b[i]>a[i]\) 的物品。

分界线前用一个优先队列维护，分界线后预处理一个后缀和作为贡献。

时间复杂度 \(O(n\log n)\)。

CF2067E. White Magic

*1900 Code

首先，答案序列中最多出现一个 \(0\)。

• 若出现两个 \(0\)，设下标分别为 \(i,j\)。则 \(\min(a_1,\cdots,a_i)=0<1\le\text{mex}(a_{i+1},\cdots,a_j=0,\cdots,a_n)\)，矛盾。

并且，如果答案序列中有 \(0\)，这个 \(0\) 一定是左数第一个 \(0\)。

• 贪心的想，这样可以让尽可能长的后缀 \(\text{mex}\) 为 \(0\)，不劣。

最后，所有非 \(0\) 的数构成的序列一定 magical。

设有 \(cnt\) 个 \(i\) 满足 \(a_i>0\)，我们只需检查含有第一个 \(0\) 和所有非 \(0\) 数的序列。若其 magical，答案是 \(cnt+1\)；否则答案是 \(cnt\)。

时间复杂度 \(O(n)\)。

CF2067F. Bitwise Slides

*2300 Code

记 \(pre_i=\oplus_{j=1}^{i}a_j\)。

首先，操作 \(i\) 次后，有 \(P\oplus Q\oplus R=pre_i\)。三个变量 not pairwise distinct 意味着至少有两个变量相等。然而无论有两个还是三个变量相等，都会有至少一个变量等于 \(pre_i\)。

不妨设相等的两个变量为 \(x\)，操作 \(i\) 次后的状态只能是 \((pre_i,x,x),(x,pre_i,x),(x,x,pre_i)\) 中的一种。

令 \(dp[i][x]\) 表示操作 \(i\) 次后达到上述三种状态的方案数。它可以从 \((pre_i\oplus a_i,x,x),(x\oplus a_i,pre_i,x),(x\oplus a_i,x,pre_i)\) 转移而来，我们研究转移方程应该长什么样。

• 上一个状态是 \((pre_i\oplus a_i,x,x)=(pre_{i-1},x,x)\)。
  • 若 \(pre_{i-1} \neq x\)，\(dp[i][x]=dp[i-1][x]\)。
  • 否则，\(dp[i][x]=3\cdot dp[i-1][x]\)。
• 上一个状态是 \((x\oplus a_i,pre_i,x)\)。由其中两个元素相同得到 \(pre_i=x\) 或 \(pre_i=x\oplus a_i\to pre_{i-1}=x\)。
  • 若 \(pre_i=x\)，\((x\oplus a_i,pre_i,x)=(pre_{i-1},x,x)\)，故 \(dp[i][x]=dp[i-1][x]\)。
  • 若 \(pre_{i-1}=x\)，\((x\oplus a_i,pre_i,x)=(pre_i,pre_i,pre_{i-1})\)。故 \(dp[i][x]=dp[i-1][pre_i]\)。
• 上一个状态是 \((x\oplus a_i,x,pre_i)\)，同上一种。

综上，只有 \(pre_{i-1}=x\) 时 \(dp[i][x]\) 不从 \(dp[i-1][x]\) 转移而来。

此时 \(dp[i][x]=3\cdot dp[i-1][x]+2\cdot dp[i-1][pre_i]\)。

把第一维压掉，第二维 \(x\) 换成 \(pre_{i-1}\)，得到转移方程： \[ dp[pre_{i-1}]=3\cdot dp[pre_{i-1}]+2\cdot dp[pre_i] \] 初始 \(dp[0]=1\)，用 std::map 作容器，时间复杂度 \(O(n\log n)\)。

CF2064E. Mycraft Sand Sort

*2400 Code

首先注意到 \(\{c\}\) 的顺序不能换，因为第一列是不会下落的，换了之后第一列肯定不同。

结论：对于一组 \(p_i,p_j\)，它们能交换位置当且仅当 \(c_i=c_j\) 且 \(\max\limits_{k\in (i,j),c_k \neq c_i}p_k < \min(p_i,p_j)\)。

• 若 \(c_i \neq c_j\)，交换会改变颜色的相对顺序，一定不合法。
• 若 \(\max\limits_{k\in (i,j),c_k \neq c_i}p_k > \min(p_i,p_j)\)，令 \(p_m=\max\limits_{k\in (i,j),c_k \neq c_i}p_k\)，不难想象交换前后在 \(p_m\) 上侧颜色 \(c_i\) 的数目肯定不同。

那么如何计数呢？考虑 \(1\sim n\) 的一个排列，每次删去一个数相当于固定的 \(\{p\}\) 的一位，删除序列和原排列构成双射，因此我们只用对删数的方式进行计数。

将 \(p_i\) 从小到大枚举，统计完之后把 \(i\) 这个位置删掉，两端用双向链表连接。这么做的好处是统计到 \(p_i\) 时能与 \(p_i\) 交换的行一定相邻（不相邻只能是中间夹着更短的，但更短的已经在这之前被删掉了），形成一个连通块。假设此时 \(p_i\) 所在的连通块大小是 \(t_i\)，依据乘法原理最终答案就是 \(\prod t_i\)。

用并查集维护连通块大小。时间复杂度 \(O(n\log n)\)。

CF2069E. A, B, AB and BA

*2300 Code

"AA" 和 "BB" 是不被允许的。我们在相邻的两个 "A"，相邻的两个 "B" 中间划一刀，这样整个序列被分割成若干子串，每个子串是下列四种之一：

• ABAB...AB;
• BABA...BA;
• ABAB...ABA;
• BABA...BAB.

对于长为 \(l\) 的第三第四类子串，可以用 \(\frac{l-1}{2}\) 个 AB 或 BA 填充，剩下的一定是一个 A（如果是第三类）或者一个 B（如果是第四类）。此时 AB 和 BA 的地位等价。

对于长为 \(l\) 的第一类子串，可以用 \(\frac{l}{2}\) 个 AB 完全填充，或 \(\frac{l}{2}-1\) 个 BA 外加一个 A 和一个 B。此时 AB 的地位显然高于 BA。同理对于第二类子串，BA 的地位高于 AB。

对于第一第二类子串，只有用 AB（或 BA）完全填满才不会浪费，所以我们的决策顺序是：

• 用 AB 填充长度最小的第一类串，直到 AB 不足或没有第一类串了。
• 用 BA 填充长度最小的第二类串，直到 BA 不足或没有第二类串了。
• 用 BA，A，B 填充第一类串的剩余部分。
• 用 AB，A，B 填充第二类串的剩余部分。
• 用剩下的 AB，BA，A，B 填充第三第四类串。

若填充过程缺材料了，就是 NO。

时间复杂度 \(O(n\log n)\)。

CF2069F. Graph Inclusion

*2800 Code

断言：任何时刻，答案是 \(A\) 的连通块数减去 \(A\cup B\) 的连通块数。

• 挺显然的。

然后就是线段树分治板子了。

时间复杂度 \(O(q\log^2 q)\)。