【题解】2025 UESTCPC 初赛

据说题比去年初赛要简单，但我去年抱上了 lyc 大腿，所以完全不记得去年难度怎么样了。

今年来验题，但水平有限（集训队垫底水平），只验了一些简单题。

其中 A 题是经出题人提醒做出来的，D 偷看了 Tag，H 和 L 则完全不会，等有出题人题解了我再补上来。代码都写的很唐，也不一定是最优解，不要笑话我QAQ。

主观难度分布（H、L 未做出）：

签到：F，G，J，N。
Easy：B，C，I，O，P。
Easy_Mid：K，M。
Mid：D，E，Q。
Mid_Hard：\(\varnothing\)。
Hard：A。

写下这段话的时候还有三天才初赛，大胆猜测决赛线是 \(4\) 题（签到即送）。

（upd on 04.01）大一队伍 4 题，非大一队伍 5 题，外校未知。

（upd on 赛后）按榜来看 H 是 Easy/Easy_Mid，L 是 Mid_Hard/Hard。

（upd on 03.31）来点链接。

补题链接：Cdoj。

题面：Statement。

官方题解：Solution。

查重前榜单：Scoreboard。

（upd on 赛后）来点 Statistics。

本场比赛共有 405 支队伍报名，其中正式队 278 支，打星队 127 支。

有效参赛队伍（至少通过 \(1\) 题）总计 309 支，其中正式队 212 支，打星队 97 支。

最终 3 支队伍 AK，过题数情况如下。

组别 \| 过题数	17	16	15	14	13	12	11	10
正式队	1	0	0	0	1	0	2	4
打星队	2	0	1	2	2	8	8	6

组别 \| 过题数	9	8	7	6	5	4	3	2	1
正式队	9	14	8	14	23	14	56	35	31
打星队	6	3	8	10	9	5	17	6	4

接收到 8978 份有效 submissions，1698 份答案正确。

（upd on 初赛日）来点赛时趣事：

08:58 哎我草怎么是我发题面，赶紧登上 dj 下了个发到群里。

09:20 卧槽了，C 怎么被暴力过了，还碾压 std。验题的时候不交暴力导致的。

09:43 大哥给 C 加了一组数据，好很多了。

10:03 哎哎，I 的精度被浮点数硬抗过去了，精度大师。

10:47 Queue 莫名其妙 5min 了，有点爆了。

10:55 Queue 越来越长了，爆爆爆，准备多搞几台服务器加 judgehost。

11:20 加了一台 8c16g 开了 8 个 judgehost，把原来的关掉了，只跑 web。

11:27 貌似有点好转（？）

11:31 好起来了。终于有时间看榜，发现 M 竟然还没人过啊，低估了。

Fun Fact：在 pool 里 M 的难度是 *1300，有点幽默。

11:41 DeepSleep 这么厉害啊，队里两个 2000+ 就是不一样。

11:52 网页 502 了？？？？

11:55 k4c 很快就发现 /etc/php/8.2/fpm/pool.d/domjudge.conf 里 request_slowlog_timeout 的值写成了 10si，多了个 i。改完马上又好了。

12:01 L 被开出来了啊。你知道的，我一直是 DeepSleep 的粉丝。

下午就比较清闲了，大概就是时不时把 judgehost 的 internal error 给 resolved 一下。

本来想润去打洛谷的蓝桥杯模拟赛，斟酌了一下还是算了。

这期间 QQ 收到了若干人机大学生发来的弱智让人啼笑皆非的私信。

15:37 sooke 拿到了 first AK!

16:58 第一发交 clar 的代码出现了。

不知道会不会有往 clar 里交奶龙的，很期待啊！

19:08 DeepSleep 也 AK 了，仿佛看到了泥电的下一支 wf 队。

20:10 爆爆爆，O 被乱搞搞过去了。更有戏剧性的是我看出题人的题解，突然发现我验题的时候写了个错解（下面改正了），太难绷了。

在这里给大伙磕头了。

A. 炼金术士

拉姆齐定理指出，\(6\) 个点的完全图（\(K_6\)）用两种颜色任意着色（每条边都必须着色），必然存在至少一个单色三角形。

这意味着我们选出的 "黑化边" 与 "白化边" 并集的边导出子图一定不含 \(K_6\)。

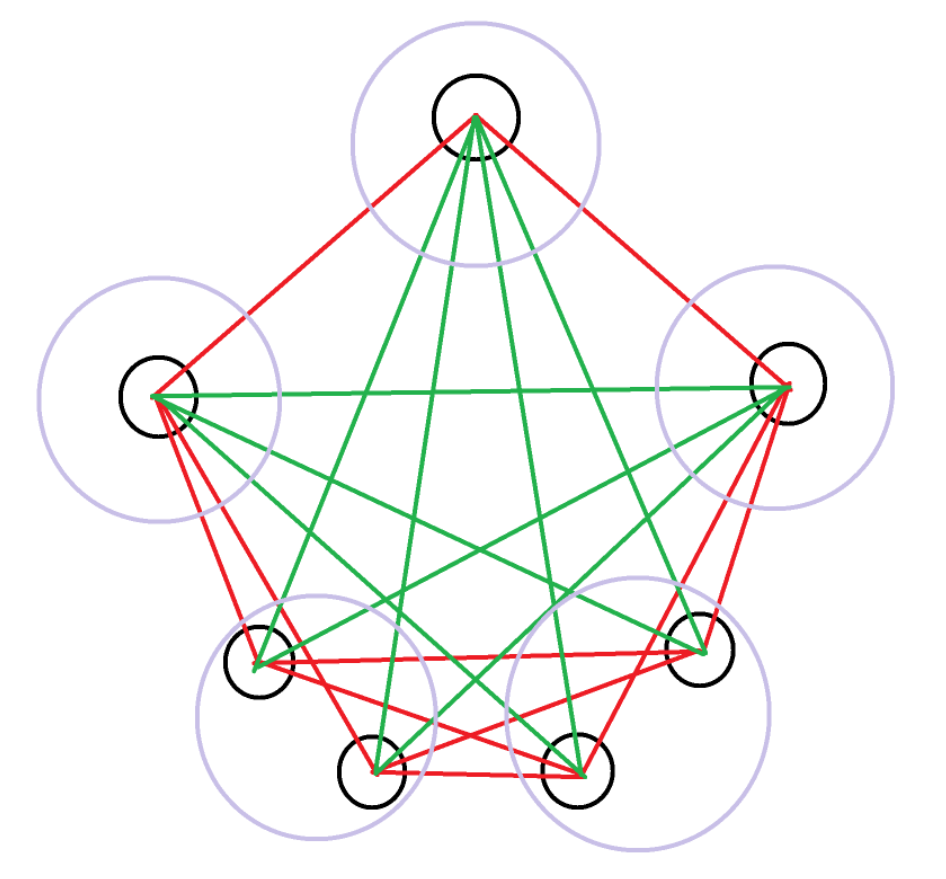
发扬人类智慧，考虑这么一种构造：将 \(n\) 个点划分成尽可能平均的 \(5\) 个集合，每个集合内部互不连边，不同集合间全部连边。

根据抽屉原理，从中任意选出 \(6\) 个点，至少有 \(2\) 个来自同一集合，没有连边，故不含 \(K_6\)。在此基础上，容易说明这样的构造具有最大连边数。

接着，我们要将这些边划分成两个集合，每个集合不含三元环，且其中一个集合能塞得下给定的长度为 \(k\) 的无环链。

再度发扬人类智慧，给上述 \(5\) 个点集编号 \(0\sim 4\)，进行如下构造：

"黑化边"：点集 \(i\) 中的所有点向点集 \((i+1)\bmod 5\) 中的所有点连出的边。
"白化边"：剩下的所有边。

因为一个三元环肯定有一条边的两个端点不来自相邻的点集，故 "黑化边" 不含三元环。

而 "白化边" 要满足 "任意一条边都不来自相邻点集"，则至少需要 \(6\) 个点集，不满足。

此外，在这 \(5\) 个点集上绕圈圈，一定能构造出一条包含所有 \(n\) 个顶点的链，将给定的链随便插进一个位置即可。

时间复杂度 \(O(n^2)\)。

上图是 \(n=7\) 的图例，\(5\) 个集合的大小分别为 \(2, 2, 1, 1, 1\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, k;
	cin >> n >> k;
	vector<int> a(k + 1);
	for (int i = 0; i <= k; i++) {
		cin >> a[i];
	}
	vector<vector<int>> b(5);
	vector<int> bel(n + 1);
	{
		vector<bool> vis(n + 1);
		int cur = 0;
		for (auto x : a) {
			b[cur].push_back(x);
			bel[x] = cur;
			cur = (cur + 1) % 5;
			vis[x] = true;
		}
		for (int i = 1; i <= n; i++) {
			if (!vis[i]) {
				b[cur].push_back(i);
				bel[i] = cur;
				cur = (cur + 1) % 5;
			}
		}
	}
	vector vis(n + 1, vector<int>(n + 1));
	for (int i = 0; i < 5; i++) {
		int j = (i + 1) % 5;
		for (auto x : b[i]) {
			for (auto y : b[j]) {
				vis[x][y] = vis[y][x] = 1;
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = i + 1; j <= n; j++) {
			if (bel[i] != bel[j] && vis[i][j] == 0) {
				vis[i][j] = vis[j][i] = 2;
			}
		}
	}
	int ans = 0;
	for (int i = 2; i <= n; i++) {
		for (int j = 1; j < i; j++) {
			ans += (vis[i][j] > 0);
		}
	}
	cout << ans << "\n";
	for (int i = 2; i <= n; i++) {
		for (int j = 1; j < i; j++) {
			if (vis[i][j] == 1) {
				cout << '+';
			} else if (vis[i][j] == 2) {
				cout << '-';
			} else {
				cout << '0';
			}
		}
		cout << "\n";
	}
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

B. 简单可满足性问题

假定已经将所有变量赋过了值，可以分出以下三类子句。

该子句所有变量均为 \(1\)，此时子句的值为 \(1\)。
该子句所有变量均为 \(0\)，此时子句的值为 \(0\)。
该子句部分变量为 \(1\)，此时子句的值为 \(1\)。

注意到当我们给所有变量取反时，第一和第二类子句个数互换，第三类子句个数不变。

而 "第一 + 第三" 类子句的个数和 "第二 + 第三" 类子句的个数总有一个 \(\ge \lceil\frac{m}{2}\rceil\)。

给所有变量任意赋值，验证不满足后就全部取反，总有一个满足条件。

时间复杂度 \(O(m)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, m;
	cin >> n >> m;
	int res = 0;
	for (int i = 0; i < m; i++) {
		int num;
		cin >> num;
		int ok = 0;
		for (int j = 0; j < num; j++) {
			int x, y;
			cin >> x >> y;
			ok |= y;
		}
		if (ok) {
			res++;
		}
	}
	int ans = 1;
	if (res * 2 < m) {
		ans = 0;
	}
	for (int i = 0; i < n; i++) {
		cout << ans << " \n"[i == n - 1];
	}
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

C. 箭串

将询问离线。暴力做就是倒序遍历每个区间，如果是 *，就覆盖；否则不操作。

用 std::set 维护当前还存活的 * 的位置。对于一个询问 \([l,r]\)，二分出 std::set 中第一个 \(\ge l\) 的位置，迭代器一直向右，修改沿途位置即可。

时间复杂度 \(O((n+m)\log n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, m;
	cin >> n >> m;
	string s = string(n + 1, '*');

	vector<array<int, 2>> op;
	for (int i = 0; i < m; i++) {
		int x, y;
		cin >> x >> y;
		op.push_back({x, y});
	}
	reverse(op.begin(), op.end());

	vector<int> L(n + 2), R(n + 2);
	set<int> t;
	for (int i = 1; i <= n; i++) {
		L[i] = i - 1;
		R[i] = i + 1;
		t.insert(i);
	}
	auto del = [&] (int i) {
		t.erase(i);
		L[R[i]] = L[i];
		R[L[i]] = R[i];
	}; 

	for (auto [p, l] : op) {
		auto it = t.lower_bound(p);
		if (it == t.end()) {
			continue;
		}
		for (int i = *it; i <= p + l - 1; i = R[i]) {
			if (i == p || i >= p + l - 3) {
				s[i] = '>';
			} else {
				s[i] = '-';
			}
			del(i);
		}
	}

	s = s.substr(1);
	cout << s << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

D. 阿罗祖斯坦的桥

令 \(f[l][r],g[l][r]\) 分别表示在 \([l,r]\) 里建桥的最大数量和最小总长度，然后就是一个裸的区间 dp。

发现 \(w(l,r)=d\cdot \text{arcsin}(\frac{\text{dis}(l,r)}{d})\) 具有单调性（跨度大桥更长）和四边形不等式条件（交叉弱于包含），于是套一个四边形不等式优化的板子就过了。

时间复杂度 \(O(n^2)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


constexpr double eps = 1e-10;

void solve() {
    int n, d;
    cin >> n >> d;
    vector<int> a(n + 1), pre(n + 2);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        pre[i + 1] = pre[i] + a[i];
    }
    auto cost = [&] (int l, int r) -> double {
        return 1.0 * d * asin(1.0 * (pre[r] - pre[l]) / d);
    };
    auto ok = [&] (int l, int r) -> bool {
        return pre[r] - pre[l] <= d;
    };
    vector f(n + 2, vector<int>(n + 2)), m(f);
    vector g(n + 2, vector<double>(n + 2));
    for (int i = 1; i <= n + 1; i++) {
        m[i][i] = i;
        if (i < n + 1) {
            m[i][i + 1] = i;
        }
    } 
    for (int len = 2; len <= n + 1; len++) {
        for (int i = 1; i + len - 1 <= n + 1; i++) {
        	int j = i + len - 1;
            for (int k = m[i][j - 1]; k <= m[i + 1][j]; k++) {
                if (f[i][k] + f[k][j] > f[i][j]) {
                    f[i][j] = f[i][k] + f[k][j];
                    g[i][j] = g[i][k] + g[k][j];
                    m[i][j] = k;
                } else if (f[i][k] + f[k][j] == f[i][j]) {
                    if (g[i][k] + g[k][j] < g[i][j]) {
                        g[i][j] = g[i][k] + g[k][j];
                        m[i][j] = k;
                    }
                }
            }
            if (ok(i, j)) {
                f[i][j]++;
                g[i][j] += cost(i, j);
            }
        }
    }
    cout << fixed << setprecision(12) << g[1][n + 1] << "\n";
}


signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T = 1;
    while (T--) {
        solve();
    }
    return 0;
}

E. 猫猫城大选（困难版）

把问题 format 一下：给定一个变量 \(x\)，初始为 \(0\)，四种操作如下，问最终 \(x\) 的期望。

\(x\leftarrow x+1\)；
\(x\leftarrow x-1\)；
\(\begin{cases}x\leftarrow x+1 &,x>0\\ x\leftarrow x-1&,x<0\\ p_i \text{ 概率}+1,(1-p_i)\text{ 概率}-1 &,x=0\end{cases}\)
\(\begin{cases}x\leftarrow x-1 &,x>0\\ x\leftarrow x+1&,x<0\\ p_i \text{ 概率}+1,(1-p_i)\text{ 概率}-1 &,x=0\end{cases}\)

我们发现对于两个 \(x=0\) 的位置，其间进行的操作是确定的。

具体的，假设当前时刻操作前 \(x=0\) 且当前为第 \(3/4\) 类操作：若选择了 \(+1\)，则直到下一次 \(x=0\) 之前 \(x\) 的值都是正的；若选择了 \(-1\)，则直到下一次 \(x=0\) 之前 \(x\) 的值都是负的。

令 \(dp[i]\) 代表若第 \(i\) 个时刻操作前 \(x=0\)，最后 \(x\) 的期望值。

从后向前转移，\(dp[i]=p[i]\cdot f(i)+(1-p[i])\cdot g(i)\)。

其中 \(f(i)/g(i)\) 代表第 \(i\) 时刻选择了 \(+1/-1\) 的情况下，之后的贡献。

以 \(f(i)\) 为例，若之后不存在 \(x=0\) 的时刻，\(f(i)=a_n-a_i+1\)，其中 \(a_i\) 表示假定 \(x\) 一直 \(>0\)，按顺序执行完第 \(i\) 次操作后的结果；否则设这 \(i\) 之后第一个 \(x=0\) 的时刻为 \(\text{nxt}\)，有 \(f(i)=dp[\text{nxt+1}]\)。

找 \(\text{nxt}\) 的过程可以用线段树实现，时间复杂度 \(O(n\log n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff

template<class T>
constexpr T power(T a, int b) {
    T res = 1;
    for (; b; b /= 2, a *= a)
        if (b % 2) res *= a;
    return res;
}
constexpr int mul(int a, int b, int p) {
    int res = a * b % p;
    if (res < 0) res += p;
    return res;
}
template<int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(int x) : x{norm(x % getMod())} {}
    static int Mod;
    constexpr static int getMod() { return P > 0 ? P : Mod;}
    constexpr static void setMod(int Mod_) { Mod = Mod_;}
    constexpr int norm(int x) const { if (x < 0) x += getMod(); if (x >= getMod()) x -= getMod(); return x;}
    constexpr int val() const { return x;}
    explicit constexpr operator int() const { return x;}
    constexpr MInt operator-() const { MInt res; res.x = norm(getMod() - x); return res;}
    constexpr MInt inv() const { assert(x != 0); return power(*this, getMod() - 2);}
    constexpr MInt &operator*=(MInt rhs) & { x = mul(x, rhs.x, getMod()); return *this;}
    constexpr MInt &operator+=(MInt rhs) & { x = norm(x + rhs.x); return *this;}
    constexpr MInt &operator-=(MInt rhs) & { x = norm(x - rhs.x); return *this;}
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv();}
    friend constexpr MInt operator*(MInt lhs, MInt rhs) { MInt res = lhs; res *= rhs; return res;}
    friend constexpr MInt operator+(MInt lhs, MInt rhs) { MInt res = lhs; res += rhs; return res;}
    friend constexpr MInt operator-(MInt lhs, MInt rhs) { MInt res = lhs; res -= rhs; return res;}
    friend constexpr MInt operator/(MInt lhs, MInt rhs) { MInt res = lhs; res /= rhs; return res;}
    friend constexpr istream &operator>>(istream &is, MInt &a) { int v; is >> v; a = MInt(v); return is;}
    friend constexpr ostream &operator<<(ostream &os, const MInt &a) { return os << a.val();}
    friend constexpr bool operator==(MInt lhs, MInt rhs) { return lhs.val() == rhs.val();}
    friend constexpr bool operator!=(MInt lhs, MInt rhs) { return lhs.val() != rhs.val();}
};

template<>
int MInt<0>::Mod = 998244353;

template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int modp = 998244353;
using Z = MInt<modp>;

// template<int P>
// int MInt<P>::Mod = P;

// using Z = MInt<0>;
// Z::setMod(mod);

template<class Info>
struct SegmentTree {
	int n;
	vector<Info> tr;
	SegmentTree(vector<int> &a) {
		vector<Info> b(a.size());
		for (int i = 0; i < a.size(); i++) {
			b[i] = a[i];
		}
		init(b);
	}
	SegmentTree(vector<Info> &a) {
		init(a);
	}
	void init(vector<Info> &a) {
		n = a.size() - 1;
		tr.assign((4 << __lg(n + 1)) + 5, Info());
		build(1, 1, n, a);
	}
	#define ls (p << 1)
	#define rs (p << 1 | 1)
	void build(int p, int l, int r, vector<Info> &a) {
		if (l == r) {
			tr[p] = a[l];
			return ;
		}
		int m = l + r >> 1;
		build(ls, l, m, a);
		build(rs, m + 1, r, a);
		pushup(p);
	}
	void pushup(int p) {
		tr[p] = tr[ls] + tr[rs];
	}
	void modify(int p, int l, int r, int pos, const Info &x) {
		if (l == r) {
			tr[p] = x;
			return;
		}
		int m = l + r >> 1;
		if (pos <= m) {
			modify(ls, l, m, pos, x);
		} else {
			modify(rs, m + 1, r, pos, x);
		}
		pushup(p);
	}
	void modify(int pos, const Info &x) {
		modify(1, 1, n, pos, x);
	}
	Info query(int p, int l, int r, int ql, int qr) {
		if (l > qr || r < ql) {
			return Info();
		}
		if (ql <= l && qr >= r) {
			return tr[p];
		}
		int m = l + r >> 1;
		return query(ls, l, m, ql, qr) + query(rs, m + 1, r, ql, qr);
	}
	Info query(int ql, int qr) {
		return query(1, 1, n, ql, qr);
	}
	template<class F>
	int findFirst(int p, int l, int r, int ql, int qr, F &&pred) {
		if (l > qr || r < ql) {
			return -1;
		}
		if (ql <= l && qr >= r && !pred(tr[p])) {
			return -1;
		}
		if (l == r) {
			return l;
		}
		int m = l + r >> 1;
		int res = findFirst(ls, l, m, ql, qr, pred);
		if (res == -1) {
			res = findFirst(rs, m + 1, r, ql, qr, pred);
		}
		return res;
	}
	template<class F>
	int findFirst(int ql, int qr, F &&pred) {
		if (ql > qr) {
			return -1LL;
		}
		return findFirst(1, 1, n, ql, qr, pred);
	}
	template<class F>
	int findLast(int p, int l, int r, int ql, int qr, F &&pred) {
		if (l > qr || r < ql) {
			return -1;
		}
		if (ql <= l && qr >= r && !pred(tr[p])) {
			return -1;
		}
		if (l == r) {
			return l;
		}
		int m = l + r >> 1;
		int res = findLast(rs, m + 1, r, ql, qr, pred);
		if (res == -1) {
			res = findLast(ls, l, m, ql, qr, pred);
		}
		return res;
	}
	template<class F>
	int findLast(int ql, int qr, F &&pred) {
		if (ql > qr) {
			return -1LL;
		}
		return findLast(1, 1, n, ql, qr, pred);
	}
	#undef ls
	#undef rs
};

struct Info {
	int mx = -inf;
	int mn = inf;
	Info() {}
	Info(int x) {
		mx = x;
		mn = x;
	}
};
Info operator+(const Info &a, const Info &b) {
	Info c;
	c.mx = max(a.mx, b.mx);
	c.mn = min(a.mn, b.mn); 
	return c;
};

//-------------- templates above --------------


void solve() {
	int n;
	cin >> n;
	vector<int> op(n + 1);
	vector<Z> p(n + 1);
	for (int i = 1; i <= n; i++) {
		cin >> op[i] >> p[i];
	}
	vector<int> pa(n + 1), pb(n + 1);
	for (int i = 1; i <= n; i++) {
		pa[i] = pa[i - 1];
		pb[i] = pb[i - 1];
		if (op[i] == 1) {
			pa[i]++;
			pb[i]++;
		} else if (op[i] == 2) {
			pa[i]--;
			pb[i]--;
		} else if (op[i] == 3) {
			pa[i]++;
			pb[i]--;
		} else {
			pa[i]--;
			pb[i]++;
		}
	}
	SegmentTree<Info> sa(pa), sb(pb);
	vector<Z> dp(n + 2);
	for (int i = n; i >= 1; i--) {
		auto getP = [&] () -> Z {
			int pos = sa.findFirst(i + 1, n, [&] (auto A) {
				return A.mn <= pa[i - 1] - 2 * (op[i] == 4);
			});
			if (pos == -1) {
				return pa[n] - pa[i] + 1;
			}
			return dp[pos + 1];
		};
		auto getN = [&] () -> Z {
			int pos = sb.findFirst(i + 1, n, [&] (auto A) {
				return A.mx >= pb[i - 1] + 2 * (op[i] == 4);
			});
			if (pos == -1) {
				return pb[n] - pb[i] - 1;
			}
			return dp[pos + 1];
		};
		dp[i] = p[i] * getP() + (1 - p[i]) * getN();
	}
	cout << dp[1] << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

F. 我知道你姓啥！

竖着看，相当于 \(m\) 个长为 \(n\) 的字符串。我们的目标是使这 \(m\) 个字符串互不相同。

一次添加操作相当于给每个字符串末尾添上 \(0\) 或 \(1\)。对于两个相同的字符串，在其末尾一个添 \(0\)，一个添 \(1\)，就能让它们不同。

用 std::map 统计出原来的 \(m\) 个字符串中出现次数最多的串，设其出现次数为 \(c\)。一次操作能让 \(c\leftarrow \lceil\frac{c}{2}\rceil\)，暴力模拟即可。

时间复杂度 \(O(nm\log m)\)。

Fun Fact：赛前出题人打算把 std::unordered_map 卡掉，但因为是签到，所以后来觉得没有必要就没卡。

Bonus：可以用 Trie 做到 \(O(nm)\)。

Fun Fact2：你可能会因为看到我 F 和 P 的题解和官方题解一模一样，然后联想到我是出题人。这是错的，出题人只是不想写题解了就让我发一份上去。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, m;
	cin >> n >> m;
	vector<string> s(n);
	for (int i = 0; i < n; i++) {
		cin >> s[i];
	}
	map<string, int> mp;
	for (int j = 0; j < m; j++) {
		string t;
		for (int i = 0; i < n; i++) {
			t += s[i][j];
		}
		mp[t]++;
	}
	int mx = 0;
	for (auto [_, x] : mp) {
		mx = max(mx, x);
	}
	int ans = 0;
	while (mx != 1) {
		mx = (mx + 1) / 2;
		ans++;
	}
	cout << ans << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

G. 猜数游戏

可以找到 \(\ge l\) 的最小的满足 \(x\bmod p=a\) 的位置 \(i\)，判断 \(i\) 是否 \(\le r\)。

令 \(i=kp+a\ge l\)，得 \(k\ge \lceil\frac{l-a}{p} \rceil\)，故 \(i=\lceil\frac{l-a}{p}\rceil p+a\)。

时间复杂度 \(O(1)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int a, p, l, r;
	cin >> a >> p >> l >> r;
	int x = (l - a + p - 1) / p * p + a;
	if (x <= r) {
		cout << "Yes " << x << "\n";
	} else {
		cout << "No\n";
	}
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

H. 独立事件

(upd on 03.31)

当 \(P(A)=0/1\) 时，答案是 trivial 的。否则，存在以下推导： \[ \begin{align} &P(A)P(B_I)=P(A\cap B_I)\\ \rightarrow\ &P(B_I\mid A)=P(B_I\mid \overline{A}) \\ \rightarrow\ &\frac{P(AB_I)}{P(A)}=\frac{P(\overline{A}B_I)}{P(\overline{A})} \end{align} \]

记 \(f[i]\) 表示在事件 \(A\) 对应的集合中选出元素总和为 \(i\) 的方案数。

记 \(g[i]\) 表示在事件 \(\overline{A}\) 对应的集合中选出元素总和为 \(i\) 的方案数。

那么答案是：

\[ \sum_{i=0}^{1000}\sum_{j=0}^{1000}f[i]\cdot g[j]\cdot [\frac{i}{P(A)}=\frac{j}{P(\overline{A})}] \]

其中，\(P(A)=\dfrac{\sum\limits_{i=1}^{k}a_i}{1000}\)，\(P(\overline{A})=1-P(A)\)。

\(f[i]\) 和 \(g[i]\) 可以分别用 \(01\) 背包求出。

时间复杂度 \(O(nw+w^2)\)，\(w\) 为值域。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff

template<class T>
constexpr T power(T a, int b) {
    T res = 1;
    for (; b; b /= 2, a *= a)
        if (b % 2) res *= a;
    return res;
}
constexpr int mul(int a, int b, int p) {
    int res = a * b % p;
    if (res < 0) res += p;
    return res;
}
template<int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(int x) : x{norm(x % getMod())} {}
    static int Mod;
    constexpr static int getMod() { return P > 0 ? P : Mod;}
    constexpr static void setMod(int Mod_) { Mod = Mod_;}
    constexpr int norm(int x) const { if (x < 0) x += getMod(); if (x >= getMod()) x -= getMod(); return x;}
    constexpr int val() const { return x;}
    explicit constexpr operator int() const { return x;}
    constexpr MInt operator-() const { MInt res; res.x = norm(getMod() - x); return res;}
    constexpr MInt inv() const { assert(x != 0); return power(*this, getMod() - 2);}
    constexpr MInt &operator*=(MInt rhs) & { x = mul(x, rhs.x, getMod()); return *this;}
    constexpr MInt &operator+=(MInt rhs) & { x = norm(x + rhs.x); return *this;}
    constexpr MInt &operator-=(MInt rhs) & { x = norm(x - rhs.x); return *this;}
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv();}
    friend constexpr MInt operator*(MInt lhs, MInt rhs) { MInt res = lhs; res *= rhs; return res;}
    friend constexpr MInt operator+(MInt lhs, MInt rhs) { MInt res = lhs; res += rhs; return res;}
    friend constexpr MInt operator-(MInt lhs, MInt rhs) { MInt res = lhs; res -= rhs; return res;}
    friend constexpr MInt operator/(MInt lhs, MInt rhs) { MInt res = lhs; res /= rhs; return res;}
    friend constexpr istream &operator>>(istream &is, MInt &a) { int v; is >> v; a = MInt(v); return is;}
    friend constexpr ostream &operator<<(ostream &os, const MInt &a) { return os << a.val();}
    friend constexpr bool operator==(MInt lhs, MInt rhs) { return lhs.val() == rhs.val();}
    friend constexpr bool operator!=(MInt lhs, MInt rhs) { return lhs.val() != rhs.val();}
};

template<>
int MInt<0>::Mod = 998244353;

template<int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int modp = 998244353;
using Z = MInt<modp>;

// template<int P>
// int MInt<P>::Mod = P;

// using Z = MInt<0>;
// Z::setMod(mod);


//-------------- templates above --------------


void solve() {
	int n, k;
	cin >> n >> k;
	vector<int> a(n + 1);
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	int S = 0, T = 0;
	for (int i = 1; i <= n; i++) {
		if (i <= k) {
			S += a[i];
		} else {
			T += a[i];
		}
	}
	vector<Z> f(S + 1), g(T + 1);
	f[0] = 1;
	g[0] = 1;
	for (int i = 1; i <= k; i++) {
		for (int j = S; j >= a[i]; j--) {
			f[j] += f[j - a[i]];
		}
	}
	for (int i = k + 1; i <= n; i++) {
		for (int j = T; j >= a[i]; j--) {
			g[j] += g[j - a[i]];
		}
	}
	Z ans = 0;
	for (int i = 0; i <= S; i++) {
		for (int j = 0; j <= T; j++) {
			if (i * T == j * S) {
				ans += f[i] * g[j];
			}
		}
	}
	cout << ans << "\n";
}


signed main() {
	fre(test);
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

I. 圆与直线交点

因为不能出现浮点数，所以整个计算过程要保留分数形式。

python 的 fraction 是简单的，能帮你自动约分，四则运算也很方便。C++ 要么手写分数类，要么另谋出路。

使用外心坐标公式求出三角形的外心坐标 \((X,Y)\)。
任取三点之一，坐标公式计算其与外心的距离，得到半径的平方 \(R^2\)。
由点到直线的距离公式，有：

\[ d=\frac{|(X-P_x)V_y-(Y-P_y)V_x|}{\sqrt{V_x^2+V_y^2}} \]

移项，两边平方，得到相切的充要条件 \([(X-P_x)V_y-(Y-P_y)V_x]^2=R^2(V_x^2+V_y^2)\)。
相交和相离改等号为不等号即可。

时间复杂度 \(O(1)\)。

Code

from fractions import *

def solve():
	x1, y1 = map(int, input().split())
	x2, y2 = map(int, input().split())
	x3, y3 = map(int, input().split())
	Px, Py = map(int, input().split())
	Vx, Vy = map(int, input().split())

	A1 = (x2 - x1) * 2
	B1 = (y2 - y1) * 2
	C1 = x2 * x2 + y2 * y2 - x1 * x1 - y1 * y1
	A2 = (x3 - x2) * 2
	B2 = (y3 - y2) * 2
	C2 = x3 * x3 + y3 * y3 - x2 * x2 - y2 * y2

	X = Fraction(C1 * B2 - C2 * B1, A1 * B2 - A2 * B1)
	Y = Fraction(A1 * C2 - A2 * C1, A1 * B2 - A2 * B1)

	dx = Fraction(x1, 1) - X
	dy = Fraction(y1, 1) - Y
	R2 = dx * dx + dy * dy
	
	V_sq = Vx * Vx + Vy * Vy
	goal = R2 * V_sq
	
	t1 = (X - Fraction(Px, 1)) * Fraction(Vy, 1)
	t2 = (Y - Fraction(Py, 1)) * Fraction(Vx, 1)
	Z = t1 - t2
	Z = Z * Z;
	O = Z - goal
	
	if O == Fraction(0):
		print("Or")
	elif O > Fraction(0):
		print("No")
	else:
		print("Yes")

def main():
	T = int(input())
	for _ in range(T):
		solve()
 
if __name__ == "__main__":
	main()

J. 创建用户

按照题意模拟即可。

C++ 使用 getline 读入一整行。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
    string tmp;
    getline(cin, tmp);
	int n = stoll(tmp);
	
	map<string, int> mp;
	for (int i = 0; i < n; i++) {
		string s;
		getline(cin, s);

		string t;
		int lst = -1;
		for (int j = 0; j < s.size(); j++) {
			if (s[j] == ' ') {
				if (lst == -1) {
					t += s.substr(0, j);
				} else {
					t += s[lst + 1]; 
				}
				lst = j;
			}
		}
		t += s[lst + 1];

		int tot = ++mp[t] - 1;
		if (tot > 0) {
			t += to_string(tot);
		}
		cout << t << "\n";
	}
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

K. 哲学之门

想好怎么枚举是重要的。

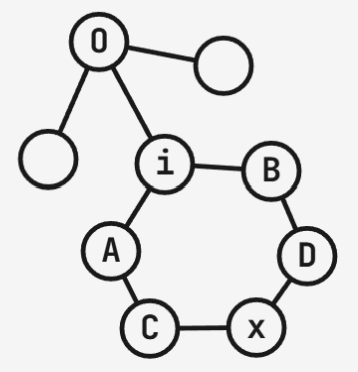
我的做法是枚举三度点 \(i\)，遍历 \(i\) 的邻接点，让每个邻居都尝试作为 \(O\)，这样 \(A,B\) 就是另外两个邻居。

再枚举 \(A\) 的邻居 \(C\)，\(B\) 的邻居 \(D\)。将 \(C\) 的邻居放进一个容器里，然后枚举 \(D\) 的邻居，若和 \(C\) 共有就是 \(x\)。

时间复杂度 \(O(n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, m;
	cin >> n >> m;
	vector<vector<int>> adj(n + 1);
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		adj[x].push_back(y);
		adj[y].push_back(x);
	}
	int ans = 0;

	vector<int> vis(n + 1);
	auto get = [&] (int i, int A, int B, int O) {
		if (adj[O].size() < 3) {
			return ;
		}
		for (auto x : adj[O]) {
			if (x == A || x == B) {
				return ;
			}
		}
		vector<int> b {O, A, B};
		for (auto x : adj[O]) {
			vis[x] = true;
			b.push_back(x);
		}
		vis[O] = true;
		vis[A] = true;
		vis[B] = true;
		set<vector<int>> res;
		for (auto C : adj[A]) {
			if (vis[C]) {
				continue;
			}
			vis[C] = true;
			set<int> s;
			for (auto x : adj[C]) {
				s.insert(x);
			}
			for (auto D : adj[B]) {
				if (vis[D]) {
					continue;
				}
				vis[D] = true;
				for (auto x : adj[D]) {
					if (vis[x]) {
						continue;
					}
					if (s.count(x)) {
						ans++;
					}
				}
				vis[D] = false;
			}
			vis[C] = false;
		}
		for (auto x : b) {
			vis[x] = false;
		}
	};

	for (int i = 1; i <= n; i++) {
		if (adj[i].size() < 3) {
			continue;
		}
		get(i, adj[i][0], adj[i][1], adj[i][2]);
		get(i, adj[i][1], adj[i][2], adj[i][0]);
		get(i, adj[i][0], adj[i][2], adj[i][1]);
	}
	cout << ans << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

M. 前兜车一转后兜车一转

选定的前缀和后缀可以是不交、恰交、相交，每种情况都讨论一下。

恰交是简单的。

不交的话预处理出 \(suf[i]\) 代表翻转 \(i\sim n\) 中的任一后缀的最大收益。接着枚举前缀，另一段的最大贡献就能查表了。

相交的话是类似的。枚举 \(i\) 代表翻转前缀 \(1\sim i\)，此时要选定一个 \(j\in [1,i]\) 然后翻转后缀 \(j\sim n\) 并让贡献最大。推一下式子，这等价于找到让 \(|a_j-a_n|-|a_j-a_{j-1}|\) 最大的 \(j\)，一样可以预处理出一个前缀和。

时间复杂度 \(O(n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n;
	cin >> n;
	vector<int> a(n + 1);
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	auto f = [&] (int i, int j) {
		return abs(a[i] - a[j]);
	};
	int res = 0;
	for (int i = 1; i < n; i++) {
		res += f(i, i + 1);
	}
	int ans = res;
	for (int i = 1; i < n; i++) {
		ans = max(ans, res - f(i, i + 1) + f(1, n));
	}
	vector<int> suf(n + 2);
	for (int i = n; i > 1; i--) {
		suf[i] = max(suf[i + 1], -f(i, i - 1) + f(n, i - 1));
	}
	for (int i = 1; i <= n - 2; i++) {
		ans = max(ans, res - f(i, i + 1) + f(1, i + 1) + suf[i + 2]);
	}
	vector<int> pre(n + 1, 0);
	for (int i = 2; i <= n; i++) {
		pre[i] = max(pre[i - 1], -f(i - 1, i) + f(i, n));
	}
	for (int i = 2; i < n; i++) {
		ans = max(ans, res - f(i, i + 1) + f(1, i + 1) + pre[i]);
	}
	cout << ans << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

N. 幸运之环 II

用 dfs 找出这棵基环树的环。

找到环上最小的点 \(x\)，再看一下 \(x\) 沿环上两个方向的邻居，哪个邻居小就往哪个方向输出。

时间复杂度 \(O(n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n;
	cin >> n;
	vector<vector<int>> adj(n + 1);
	for (int i = 1; i <= n; i++) {
		int x, y;
		cin >> x >> y;
		adj[x].push_back(y);
		adj[y].push_back(x);
	}

	vector<int> cir;
	{
		vector<int> vis(n + 1), f(n + 1), ins(n + 1);
		auto dfs = [&] (auto self, int x, int fa) -> void {
			vis[x] = true;
			ins[x] = true;
			f[x] = fa;
			for (auto y : adj[x]) {
				if (y == fa) {
					continue;
				}
				if (ins[y] && cir.empty()) {
					for (int i = x; i != y; i = f[i]) {
						cir.push_back(i);
					}
					cir.push_back(y);
				}
				if (vis[y]) {
					continue;
				}
				self(self, y, x);
			}
			ins[x] = false;
		};
		dfs(dfs, 1, 0);
	}
	int len = cir.size();
	cout << len << " ";

	cir.insert(cir.end(), cir.begin(), cir.end());
	int p = -1, mn = inf;
	for (int i = 1; i < cir.size() - 1; i++) {
		if (cir[i] < mn) {
			mn = cir[i];
			p = i;
		}
	}
	cout << cir[p] << " ";
	if (cir[p - 1] < cir[p + 1]) {
		int t = p, tot = 1;
		while (tot < len) {
			t--;
			if (t < 0) {
				t = cir.size() - 1;
			}
			cout << cir[t] << " ";
			tot++;
		}
	} else {
		int t = p, tot = 1;
		while (tot < len) {
			t++;
			if (t == cir.size()) {
				t = 0;
			}
			cout << cir[t] << " ";
			tot++;
		}
	}
	cout << "\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

O. 不走回头路

在一个强连通分量内，所有的点都可以互相到达。即同一个 SCC 内的景点可以任意安排游览顺序。

缩点，得到一个 DAG。若要能遍历所有的点，这个 DAG 必然是一条链。

在 DAG 上 dp（令 \(f[x]\) 代表以 \(x\) 结尾的链的长度的最大值），判断是否存在一个点 \(f[x]=cnt\) 即可（\(cnt\) 是缩点后的图的顶点数）。

时间复杂度 \(O(n)\)。

FunFact：一个误区是只判断缩点后的图 "恰有一个入度为 \(0\) 的点" 和 "恰有一个出度为 \(0\)" 的点，这是错误的，反例是 \(1\to 2\to 3,1\to 4\to3\)。赛时的数据有这个缺陷（包括其它一些没缩点乱搞度数的做法也过了），磕头 \(+1\)。补题链接里的数据是更新过的。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	int n, m;
	cin >> n >> m;
	vector<vector<int>> adj(n + 1);
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		adj[x].push_back(y);
	}

	vector<int> dfn(n + 1), low(n + 1), stk(n + 1), c(n + 1);
	vector<bool> vis(n + 1);
	vector<vector<int>> scc(n + 1);
	int tim = 0, top = 0, cnt = 0;
	function<void(int)> tarjan = [&](int x) {
		dfn[x] = low[x] = ++tim;
		vis[x] = true;
		stk[++top] = x;
		for (auto y : adj[x]) {
			if (!dfn[y]) {
				tarjan(y);
				low[x] = min(low[x], low[y]);
			} else if (vis[y]) {
				low[x] = min(low[x], dfn[y]);
			}
		}
		if (dfn[x] == low[x]) {
			int now; ++cnt;
			do {
				now = stk[top--];
				vis[now] = false;
				c[now] = cnt;
				scc[cnt].push_back(now);
			} while(x != now);
		}
	};
	vector<set<int>> Adj(n + 1);
	auto shrinkPoint = [&]() {
		for (int x = 1; x <= n; x++) {
			for (auto y : adj[x]) {
				if (c[x] == c[y]) continue;
				Adj[c[x]].insert(c[y]);
			}
		}
	};
	
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) {
			tarjan(i);
		}
	}
	shrinkPoint();
	
	vector<int> rd(cnt + 1);
	for (int x = 1; x <= cnt; x++) {
		for (auto y : Adj[x]) {
			rd[y]++;
		}
	}
	queue<int> q;
	vector<int> f(cnt + 1);
	for (int i = 1; i <= cnt; i++) {
		if (rd[i] == 0) {
			q.push(i);
			f[i] = 1;
		}
	}
	while (!q.empty()) {
		int x = q.front();
		q.pop();
		for (auto y : Adj[x]) {
			f[y] = max(f[y], f[x] + 1);
			if (--rd[y] == 0) {
				q.push(y);
			}
		}
	}
	if (*max_element(f.begin(), f.end()) == cnt) {
		cout << "Yes\n";
	} else {
		cout << "No\n";
	}
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T = 1;
	while (T--) {
		solve();
	}
	return 0;
}

P. 相同字符

预处理 \(pre[i]\) 代表从前向后在 \(a\) 中匹配上 \(b\) 中的字符的个数，即 \(a[0..i]\) 能匹配上 \(b[0..(pre[i]-1)]\)。

预处理 \(suf[i]\) 代表从后向前在 \(a\) 中匹配上 \(b\) 中的字符的个数，即 \(a[i..n-1]\) 能匹配上 \(b[(m-suf[i])..m-1]\)。

上述的匹配不区分大小写。

若 \(a\) 中无大写字母，判断 \(\max(suf[0],pre[n-1])=m\) 是否成立即可。

否则枚举 \(b\) 中每一个与大写字母相同的位置 \(i\)，判断 \(pre[i-1] \ge i\) 和 \(suf[i+1]\ge m-i-1\) 是否成立。

时间复杂度 \(O(n)\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
	string a, b;
	cin >> a >> b;
	int n = a.size();
	int m = b.size();

	int pos = -1;
	for (int i = 0; i < n; i++) {
		if (isupper(a[i])) {
			pos = i;
			a[i] = tolower(a[i]);
		}
	}

	vector<int> pre(n), suf(n);
	pre[0] = (a[0] == b[0]);
	suf[n - 1] = (a.back() == b.back());

	for (int i = 1; i < n; i++) {
		pre[i] = pre[i - 1];
		if (pre[i] < m) {
			pre[i] += (b[pre[i]] == a[i]);
		}
	}
	for (int i = n - 2; i >= 0; i--) {
		suf[i] = suf[i + 1];
		if (suf[i] < m) {
			suf[i] += (b[m - suf[i] - 1] == a[i]);
		}
	}

	if (pos == -1) {
		if (max(suf[0], pre[n - 1]) == m) {
			cout << "Yes\n";
			return ;
		}
	} else {
		int L = (pos == 0 ? 0 : pre[pos - 1]);
		int R = (pos == n - 1 ? 0 : suf[pos + 1]);
		for (int i = 0; i < m; i++) {
			if (b[i] == a[pos]) {
				if (L >= i && R >= m - i - 1) {
					cout << "Yes\n";
					return;
				}
			}
		}
	}
	cout << "No\n";
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

Q. 校车

数据范围识状压。将给定的 \(w\) 个路口称作关键点。

令 \(dp[S][i]\) 代表从起点出发经过了状态 \(S\) 中的点，最终到达关键点 \(i\) 所需的路程。

初态：\(dp[\{i\}][i]=\text{dis}(1,p_i)\)。
转移：\(dp[S\cup \{j\}][j]=\min(dp[S\cup \{j\}][j],dp[S][i]+\text{dis}(p_i,p_j))\)，其中 \(i\in S,j\not\in S\)。

那么经过 \(S\) 中的点再返回起点的最短距离 \(f[S]=\min\limits_{i\in S}(dp[S][i]+\text{dis}(1,p_i))\)。

二分答案，设二分出的答案是 \(mid\)，问题转化为判断是否能用不超过 \(k\) 条 \(f[S]\le mid\) 的路径覆盖所有 \(w\) 个关键点。

设 \(g[S]\) 表示覆盖 \(S\) 中的点需要的最小路径条数，判定就是 \(g[\{1,2,\ldots,w\}]\le k\)。

初态：\(g[\varnothing]=0\)。
转移：\(g[S\cup T]=\min(g[S\cup T],g[S]+1)\)，其中 \(f[T]\le mid\)。

注意：转移的时候不需要对每一个 \(S\) 都枚举所有的 \(T\)，那样是 \(O(4^w)\)。只需要 \(O(3^w)\) 枚举所有所有状态的子状态就行。

时间复杂度 \(O(wm\log m+w^22^w+20\cdot 3^{w})\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in", "r", stdin); freopen(#x".out", "w", stdout)
#define ck(x)  { cout << "check " << x << "\n"; cout.flush();}
#define int long long
#define double long double
#define inf 0x3fffffffffffffff


//-------------- templates above --------------


void solve() {
    int n, m, w, k;
    cin >> n >> m >> w >> k;
    vector<vector<array<int, 2>>> adj(n + 1);
    for (int i = 0; i < m; i++) {
        int x, y, w;
        cin >> x >> y >> w;
        adj[x].push_back({y, w});
        adj[y].push_back({x, w});
    }
    vector<int> p(w);
    for (int i = 0; i < w; i++) {
        cin >> p[i];
    }

    vector<int> dis(n + 1);
    vector d(w, vector<int>(w));
    {
        auto dijkstra = [&] (int S) {
            vector<int> dis(n + 1, inf);
            vector<bool> vis(n + 1, false);
        
            #define P pair<int, int>
            priority_queue<P, vector<P>, greater<P>> Q;
            Q.push({0, S});
            dis[S] = 0;
        
            while (!Q.empty()) {
                auto [dist, x] = Q.top();
                Q.pop();
                if (vis[x]) {
                    continue;
                }
                vis[x] = true;
        
                for (auto [y, w] : adj[x]) {
                    if (dis[y] > dist + w) {
                        dis[y] = dist + w;
                        Q.push({dis[y], y});
                    }
                }
            }
            return dis;
        };
        dis = dijkstra(1);
        for (int i = 0; i < w; i++) {
            auto A = dijkstra(p[i]);
            for (int j = 0; j < w; j++) {
                d[i][j] = A[p[j]];
            }
        }
    }
    
    vector dp(1 << w, vector<int>(w, inf));
    for (int i = 0; i < w; i++) {
        dp[1 << i][i] = dis[p[i]];
    }
    for (int S = 0; S < (1 << w); S++) {
        for (int i = 0; i < w; i++) {
            if ((S >> i & 1) == 0 || dp[S][i] == inf) {
                continue;
            }
            for (int j = 0; j < w; j++) {
                if ((S >> j & 1) == 0) {
                    int nS = S | (1 << j);
                    if (d[i][j] < 1e10) {
                        dp[nS][j] = min(dp[nS][j], dp[S][i] + d[i][j]);
                    }
                }
            }
        }
    }
    vector<int> f(1 << w, inf);
    int mx = 0;
    for (int S = 0; S < (1 << w); S++) {
        for (int i = 0; i < w; i++) {
            if ((S >> i & 1) && dp[S][i] != inf) {
                f[S] = min(f[S], dp[S][i] + dis[p[i]]);
            }
        }
        if (f[S] < 1e10) {
            mx = max(mx, f[S]);
        }
    }

    auto check = [&] (int mid) {
        vector<int> g(1 << w, inf);
        g[0] = 0;
    	for (int S = 0; S < (1 << w); S++) {
    		for (int T = S; ; T = (T - 1) & S) {
    			if (f[S ^ T] <= mid) {
    				g[S] = min(g[S], g[T] + 1);
    			}
    			if (T == 0) {
    				break;
    			}
    		}
    	}
        return g[(1 << w) - 1] <= k;
    };

    int l = 1, r = mx, ans = -1;
    while (l <= r) {
        int mid = l + r >> 1;
        if (check(mid)) {
            ans = mid;
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
    cout << ans << "\n";
}


signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T = 1;
    while (T--) {
        solve();
    }
    return 0;
}

Competitive Programming > other

#ICPC #UESTC

【题解】2025 UESTCPC 初赛

https://kisuraop.github.io/posts/94193aa7.html

作者

KisuraOP

发布于

2025年3月29日

许可协议

【题解】四月训练日记上一篇

【题解】三月训练日记下一篇