【题解】NOIP 2007 提高组
A. 统计数字
按照题意模拟即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return f==1?x:-x;
}
const int N=2e5+10;
int a[N],n;
signed main()
{
n=read();
for(int i=1;i<=n;++i) {
a[i]=read();
}
sort(a+1,a+n+1);
int tot=1;
for(int i=1;i<=n+1;++i) {
if(a[i]==a[i-1]) {
tot++;
}
if(a[i]!=a[i-1] && i!=1) {
printf("%lld %lld\n",a[i-1],tot);
tot=1;
}
}
return 0;
}B. 字符串的展开
按照题意模拟即可。
注意一些特判:
开头字符也可能为 ’ \(-\) ’。
可能有连续的 ‘ \(-\) ’。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return f==1?x:-x;
}
int p1,p2,p3;
string s;
stack<char> q;
bool check(int i)
{
if(s[i-1]=='-' || s[i]!='-' || (s[i]=='-' && i==0) ) return true;
else if((s[i]=='-') && ((int)s[i-1]>=(int)s[i+1])) return true;//'-'之后的字符ascll比前面大
else if(s[i-1]>='A' && s[i-1]<='z' && s[i+1]>='0' && s[i+1]<='9') return true;//'-'前后同为数字或字母
else if(s[i-1]>='0' && s[i-1]<='9' && s[i+1]>='A' && s[i+1]<='z') return true;
return false;
}
signed main()
{
p1=read(),p2=read(),p3=read();
cin>>s;
int lst;
for(int i=0;i<s.size();++i) {
char x=s[i];
if(x!='-' ||(x=='-' && i==0)|| check(i)) {
printf("%c",x),lst=x;
}
else {
if(i==0) {
continue;
}
lst++;
x=s[++i];
while(lst<(int)x) {
if(p1==1 || (p1==2&&(char)lst>='1'&&(char)lst<='9')) {
for(int i=1;i<=p2;++i) {
if(p3==1) {
printf("%c",(char)lst);
} else {
q.push(lst);
}
}
} else if(p1==2) {
for(int i=1;i<=p2;++i) {
if(p3==1) {
printf("%c",(char)(lst-32));
} else {
q.push(lst-32);
}
}
} else if(p1==3) {
for(int i=1;i<=p2;++i) {
printf("*");
}
lst++;
}
}
while(!q.empty()) {
printf("%c",(char)q.top());
q.pop();
}
printf("%c",x);
}
}
return 0;
}C. 矩阵取数游戏
题意:在 \(n\times m\) 的非负矩阵中取数,需要满足以下条件:
每次从每一行取走一个元素,共 \(n\) 个。经过 \(m\) 次后取完矩阵内所有元素。
每次只能在一行的行首或行尾取数。
每行取数的得分 = 被取走的元素 \(\times 2^i\),其中 \(i\) 表示第 \(i\) 次取数。最后的总得分为各行得分之和。
求最大总得分。
\(1\le n,m\le 80\),\(0\le a_{ij}\le1000\)。
不妨先观察样例:
2 3
1 2 3
3 4 282其中 \(82=2^1\times(1+2)+2^2\times(2+3)+2^3\times(3+4)\)
即 \(82=(2^1\times1+2^2\times2+2^3\times3)+(2^1\times2+2^2\times3+2^3\times4)\)
发现每行之间取数都互不干扰,即可以一行一行 dp,最后对每行答案求和。
容易想到令 \(f[i][j]\) 为左边取 \(i\) 个数,右边取 \(j\) 个数的最大得分。
故 \(f[i][j]=\max(f[i-1][j]+2^{i+j}\times a[i],f[i][j-1]+2^{i+j}\times a[m-j+1])\)。
答案为 \(\max(f[i][m-i]),i\in[1,m]\)。
爆 long long ,记得用 __int128 。
#include<bits/stdc++.h>
using namespace std;
#define int __int128
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return f==1?x:-x;
}
inline void write(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);putchar(x%10+'0');
}
inline int qpow(int k,int n) {
int s=1;
for(;n;n>>=1,k=k*k)if(n&1)s*=k;
return s;
}
const int N=100;
int n,m,a[N][N],f[N][N];
int dp(int q[])
{
memset(f,0,sizeof(f));
f[1][0]=2*q[1],f[0][1]=2*q[m];//第一次取数
for(int i=0;i<=m;++i) {
for(int j=0;i+j<=m;++j) {
f[i][j]=max(f[i-1][j]+qpow(2,i+j)*q[i],f[i][j-1]+qpow(2,i+j)*q[m-j+1]);
}
}
int maxf=0;
for(int i=0;i<=m;++i) {
maxf=max(maxf,f[i][m-i]);
}
return maxf;
}
signed main()
{
n=read(),m=read();
for(int i=1;i<=n;++i) {
for(int j=1;j<=m;++j) {
a[i][j]=read();
}
}
int ans=0;
for(int i=1;i<=n;++i) {
ans+=dp(a[i]);
}
write(ans);
return 0;
}D. 树网的核
题意:给出一颗 \(n\) 个节点的无根树,有如下定义。
偏心距(ECC) :路径 \(F\) 的 ECC 指树网中距路径 \(F\) 最远的点到路径 \(F\) 的距离。
树网的核 :在直径上找一段路径 \(F\) 使长度不超过 \(s\) 且 ECC 最小,必要时可以为一个节点。
求满足上述条件的最小 ECC 。
\(2\le n \le 300\),\(0\le s \le 10^3\),\(1\le u,v\le n\),\(0\le w \le 10^3\)。
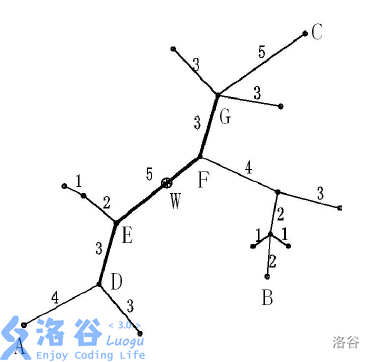
图中直径为:\(A\sim B,A\sim C\)。
若 \(s=11\),树网的核为 \(DEFG\),偏心距为 \(8\)。
若 \(s=0\sim2\),树网的核为 \(F\),偏心距为 \(12\)。
首先,可以看到 \(n\) 究极小,所以考虑暴力:
考虑找到树的直径,记录两个端点,枚举每一段长度不超过 \(s\) 的路径,逐一比较 \(ECC\)。
那么如何求一段路径的偏心距?
我们以图中 \(s=11\) 时的情况为例,树网的核为 \(DEFG\),偏心距为路径 \(BF(4+2+2=8)\)。
看图容易推出 \(dis(B,F)=( dis(B,D)+dis(G,B)-dis(D,G) )\)。
于是我们得到:\(ECC(i,j)=( dis(i,k)+dis(j,k)-dis(i,j))\div2\)。
其中 \(k\in[1,n]\),可以用一层循环枚举 \(k\),求出最小 \(ECC\)。
至于 \(dis(i,k)\),\(dis(j,k)\),\(dis(i,j)\),我们只需跑 floyd 即可。
但由于 floyd 用邻接矩阵,所以我们只能 \(O(n^2)\) 求直径,整个算法复杂度为 \(O(n^3)\)。
细节:容易得到一个点 \(k\) 在直径 \(i\sim j\) 上,那么 \(dis[i][k]+dis[k][j]=dis[i][j]\),否则 continue。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return f==1?x:-x;
}
const int N=300+10,inf=0x7fffffff;
int n,s,dis[N][N];
void init() {
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(i!=j) dis[i][j]=inf;
}
void floyd()
{
for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=dis[i][k]+dis[k][j];
}
signed main()
{
n=read(),s=read();
init();
for(int i=1;i<=n-1;++i) {
int u=read(),v=read(),w=read();
dis[u][v]=dis[v][u]=w;
}
floyd();
int pl,pr,len=0;
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
if(dis[i][j]>=inf || dis[i][j]<=len) {
continue;
}
len=dis[i][j],pl=i,pr=j;//求树的直径,记录两个端点
}
}
int ecc,ans=inf;
for(int i=1;i<=n;++i) {
if(dis[pl][i]+dis[i][pr]!=len) {
continue;
}
for(int j=1;j<=n;++j) {
if(dis[pl][j]+dis[j][pr]!=len) {
continue;
}
if(dis[i][j]>s) {
continue;
}
ecc=-inf;
for(int k=1;k<=n;++k) {
ecc=max(ecc,(dis[i][k]+dis[j][k]-dis[i][j])/2);
}
ans=min(ans,ecc);
}
}
printf("%lld",ans);
return 0;
}