[LGR-161-Div.3] 洛谷基础赛 4

A. Judg.

逐个判断即可。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read();
	for(int i=1;i<=n;++i) {
		string s;
		cin>>s;
		if(s!="AC") {
			printf("%lld ",i);
		}
	}
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		// fflush(stdout);
	}
	return 0;
}

B. Maps.

Problem

要让字典序最小，答案必然是一段前缀 \(0\) \(+\) 一段 \(01\) 交替的序列。

满状态是 \(1010\dots0101\)，所以 \(2p+1> n\) 时无解。

后续直接从后往前模拟。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;

int s[100000+5];

void solve()
{
	int n=read(),p=read();
	if(p*2+1>n) {
		puts("-1");
		return ;
	}
	int cnt=0,tot=0;
	memset(s,0,sizeof(s));
	for(int i=n;i>=1;--i) {
		if((++tot)&1) {
			s[i]=1;
		} else {
			if(++cnt==p) {
				s[i-1]=1;
				break;
			}
		}
	}
	for(int i=1;i<=n;++i) {
		printf("%lld",s[i]);
	}
	puts("");
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		// fflush(stdout);
	}
	return 0;
}

C. Colo.

Problem

好题

题意：给定个长度为 \(n\) 的序列 \(a,b\) 分别代表颜色和价值，你可以挑一些不同的颜色 \(a_i\) 进集合 \(S\) 中，获得 \(b_{a_i}\) 价值，但需要使所有 \(x\in S\) 从 \(a\) 中按顺序取出后形成的序列单调不降。求 \(|S|=k\) 时能获得的最大价值。

\(1\le n,k \le 500\)，\(1\le a_i\le n\)，\(1\le b_i\le10^9\)。

把每种不同的颜色看成一个线段 \([\text{fir}_{a[i]},\text{end}_{a[i]}]\)，其中 \(\text{fir}_{a[i]}\) 和 \(\text{end}_{a[i]}\) 分别是颜色 \(a[i]\) 第一次出现的地方和最后一次出现的地方。不难发现如果当前保留了两种及以上的颜色，那么所有线段都应该是互相隔离的（即既不包含也不相交），这样才能确保最终序列的单调性。

现在相当于确定了一种 \(a[i]\)，我们可以去区间 \([1,\text{fir}_{a[i]})\) 去寻找一个 \(\text{end}_{a[j]}\)，这样 \(a[i]\) 就可以从 \(a[j]\) 那转移过来。

这样就转化为了一个类背包问题，用 dp 求解。

令 \(dp[\text{end}_{i}][len]\) 表示目前选择到了颜色 \(i\) ，已经选了 \(len\) 种颜色。

转移方程如下：

\[\normalsize{dp[\text{end}_i][len]=\max\limits_{j=\text{end}_{a[j]}\text{ },\text{ }j\in [1,\text{fir}_i)}(dp[j][len-1]+b[i])}\]

答案即为 \(\max\limits_{i\in [1,n]}dp[i][k]\)。

有点抽象，看代码可能更直观。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read(),k=read();
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;++i) {
		a[i]=read();
	}
	for(int i=1;i<=n;++i) {
		b[i]=read();
	}
	vector<int> fir(n+1),end(n+1);
	vector<bool> vis(n+1,false);
	for(int i=1;i<=n;++i) {
		if(!vis[a[i]]) {
			vis[a[i]]=true;
			fir[a[i]]=i;
		}
		end[a[i]]=i;
	}
	vector<vector<int>> dp(n+1,vector<int>(k+1,-inf));
	for(int i=1;i<=n;++i) { //表示当前枚举到颜色i 
		if(vis[i]) {
			for(int j=1;j<fir[i];++j) {
				if(j==end[a[j]]) {
					for(int len=2;len<=k;++len) {
						if(dp[j][len-1]!=-inf) {
							dp[end[i]][len]=max(dp[end[i]][len],dp[j][len-1]+b[i]);
						}
					}
				}
			}
			dp[end[i]][1]=b[i]; //只选它自身
		}
	}
	int res=-inf;
	for(int i=1;i<=n;++i) {
		res=max(res,dp[i][k]);
	}
	if(res==-inf) {
		puts("-1");
	} else {
		printf("%lld\n",res);
	}
}


signed main()
{
	fre(test);
	int T=1;
	while(T--) {
		solve();
		// fflush(stdout);
	}
	return 0;
}

这和一般的 dp 有点不一样，所以看起来很奇怪。

我们分析它的正确性是如何保证的：

外层从小到大枚举颜色 \(i\)，保证不会从比它大的颜色转移过来，使序列单调不降。
用右端点 \(\text{end}_{i}\) 代表该种颜色，只保留有用的部分，符合最优子结构性质。

时间复杂度 \(O(n^2k)\)。

D. Bina.

Problem

毒瘤

题意：给定正整数 \(n,m\)，依照给定代码建一棵构建参数为 \(n\) 二叉树。你可以从二叉树底部开始往上砍节点（或不砍），一次砍一层，至少砍 \(m\) 个点。令美丽值 \(=\) 所有节点编号之和 \(\div\) 这棵树的深度（向下取整），求最大美丽值。

很难下手，但你可以把 \(n=1\sim 16\) 的图都手玩出来，找到一些性质。

这是 \(n=13\) 的图。

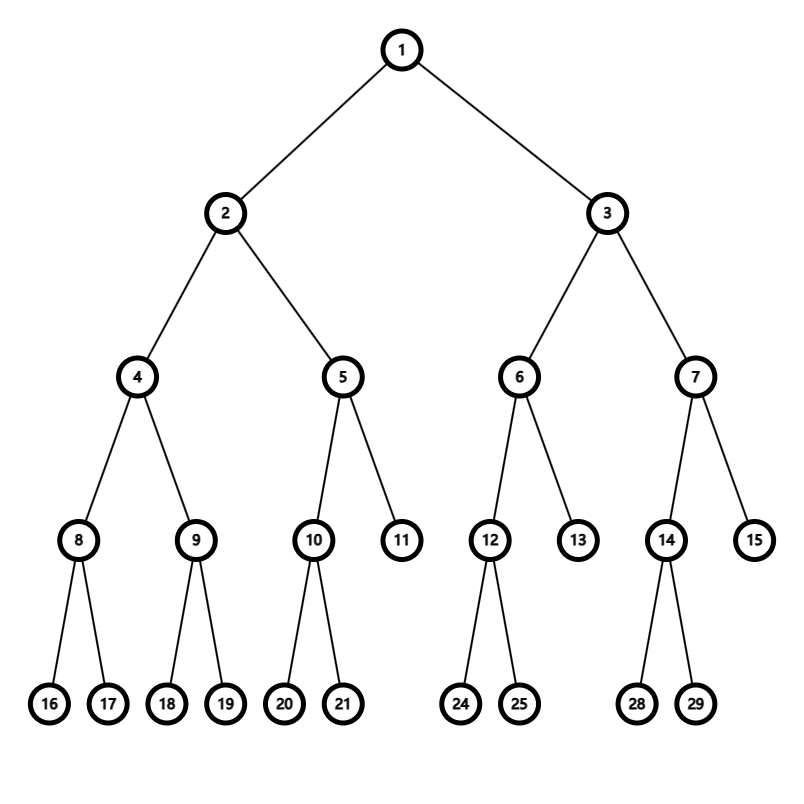最明显的是这颗树除去最后一层必然是满二叉树，而且最后一层的叶子节点必然成对出现。

再进一步，\(n\leftarrow n+1\) 时就会多出两个节点，所以总节点数量 \(2n-1\) 是已知的，进而树的深度 \(d\) 也能推出。

其次一颗 \(d\) 层的满二叉树，其美丽值为 \(\frac{(1+2^{n}-1)(2^n-1)}{2}\times \frac{1}{d}=\frac{2^{n-1}(2^n-1)}{d}\)，单调增。

意味着尽可能保留满二叉树层数是最优的。

故 \(m>0\) 时，最后一层必砍，在此基础上砍够 \(m\) 就马上停手，答案最优。

麻烦的是 \(m=0\)，这意味着答案是从砍最后一层和一点不砍之间取较大者。

前者可以预处理，后者我们需要知晓最后一层的节点编号和。

找规律。

打印出 \(n=2^3\sim 2^4\) 时是哪些编号（设为 \(x\)）的节点下挂了两个新节点。

\(n=\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)	\(13\)	\(14\)	\(15\)
\(x=\)	8	12	10	14	9	13	11	15

都减去 \(2^3\) 有：

\(n=\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
\(x=\)	0	4	2	6	1	5	3	7

此时我们发现 \(x\) 是对应 \(n\) 的二进制翻转。

设 \(k=n-2^p-1\)，\(rev(i)\) 为 \(i\) 的二进制翻转。

又由于 \(x\) 下挂的两个节点编号为 \(2x\) 和 \(2x+1\)，最后一层的总编号和即为： \[\begin{align}&\text{ }\text{ }\text{ }\sum\limits_{i=0}^{k}(((2^p+rev(i))\times 2)+(2^p+rev(i))\times2 +1)\\&=(k+1)(2^{p+2}+1)+4\sum_{i=0}^k rev(i)\end{align}\] 由表推出 \(p=d-1\)。那么如何求 \(\sum\limits_{i=0}^k rev(i)\) ？

拆位考虑，考虑 \(0\sim k\) 中每个数的第 \(x\in[0,p)\) 位为 \(1\) 的个数 \(cnt\)，对翻转后的贡献即 \(cnt\times 2^{p-x-1}\) 。

单组总时间复杂度 \(O(\log n)\)。

利用二进制下第 \(x\) 位每隔 \(2^x\) 个就改变一次的特性，统计循环节，可以 \(O(1)\) 统计每一位的 \(cnt\)。

Code

#include <bits/stdc++.h>
using namespace std;
#define fre(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout)
#define int long long
#define double long double
#define PI acos(-1)
#define inf 0x3fffffffffffffff
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
	return f==1?x:-x;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
const int modp = 998244353;


void solve()
{
	int n=read(),m=read();
	int all=2*n-1,depth=0;  //all:总节点数,depth:总深度
	while((1ll<<depth)<all) {
		depth++;
	}
	if(m>all) {
		puts("-1");
		return ;
	}
	int lastnum=all-((1ll<<(depth-1))-1); //最后一层节点数
	if(m>0) {
		int tmp=depth,cut=0;
		while(1) {
			if(tmp==depth) {
				cut+=lastnum;
			} else {
				cut+=(1ll<<(depth-1));
			}
			depth--;
			if(cut>=m) {
				break;
			}
		}
		if(!depth) {
			puts("-1");
		} else {
			int res=(1ll<<(depth-1))*((1ll<<depth)-1)/depth;
			printf("%lld\n",res);
		}
	} else {
		depth--;  //此时depth是满二叉树层数
		int res=(1ll<<(depth-1))*((1ll<<depth)-1)/depth;
		int sum=0,tmp_n=n-(1ll<<(depth-1));
		for(int i=0;i<depth-1;++i) {
			int cnt=tmp_n/(1ll<<i);
			int left=tmp_n%(1ll<<i);
			int ano_cnt=cnt;
			if(cnt&1) {
				ano_cnt--;
			}
			ano_cnt/=2;
			ano_cnt*=(1ll<<i);
			if(cnt&1) {
				ano_cnt+=left;
			}
			sum+=ano_cnt*(1ll<<(depth-i-2));
		}
		sum=tmp_n*((1ll<<(depth+1))+1)+4*sum; //操作后sum为最后一层节点编号和
		int res2=((1ll<<(depth-1))*((1ll<<depth)-1)+sum)/(depth+1);
		printf("%lld\n",max(res,res2));
	}
}


signed main()
{
	fre(test);
	int T=read();
	while(T--) {
		solve();
		//fflush(stdout);
	}
	return 0;
}

Competitive Programming > Luogu

#OI #Luogu

[LGR-161-Div.3] 洛谷基础赛 4

https://kisuraop.github.io/posts/26a0ed02.html

作者

KisuraOP

发布于

2023年10月5日

许可协议

[LGR-162-Div.3] 洛谷基础赛 5 & QFOI Round 1 上一篇

【题解】2023 NOI 春季测试 3 of 4 下一篇